Training
In optimization, we've seen how nested AD and gradient-based optimization work together.
Training a model is the optimization of model parameters to minimize a loss function, or equivalently, to maximize the likelihood of a given set of data under the model parameters. In addition to the optimization method, learning rate, momentum, and gradient clipping parameters we've seen, this introduces parameters for the loss function, regularization, training batches, and validation and early stopping.
But let's start with the Dataset type, which we will use for keeping the training, validation, and test data for the training procedure.
Dataset
For supervised training, data consists of pairs of input vectors \(\mathbf{x}_i \in \mathbb{R}^{d_x}\) and output vectors \(\mathbf{y}_i \in \mathbb{R}^{d_y}\). We represent data using the Dataset type, which is basically a pair of matrices
\[ \begin{eqnarray*} \mathbf{X} &\in& \mathbb{R}^{d_x \times n}\\ \mathbf{Y} &\in& \mathbb{R}^{d_y \times n}\\ \end{eqnarray*}\]
holding these vectors, where \(n\) is the number of input–output pairs, \(d_x\) is the number of input features and \(d_y\) is the number of output features. In other words, each of the \(n\) columns of the matrix \(\mathbf{X}\) is an input vector of length \(d_x\) and each of the \(n\) columns of matrix \(\mathbf{Y}\) is the corresponding output vector of length \(d_y\).
Keeping data in matrix form is essential for harnessing high-performance linear algebra engines tailored for your CPU or GPU. Hype, by default, uses a high-performance CPU backend using OpenBLAS for BLAS/LAPACK operations, and parallel implementations of non-BLAS operations such as elementwise functions.
1: 2: 3: 4: 5: 6: 7: 8: |
|
Hype provides several utility functions for loading data into matrices from images, delimited text files (e.g., CSV), or commonly used dataset files such as the MNIST.
1: 2: 3: 4: 5: |
|
You can see the API reference and the source code for various ways of constructing Datasets.
Training parameters
Let's load the housing prices dataset from the Stanford UFLDL Tutorial and divide it into input and output pairs. We will later train a simple linear regression model, to demonstrate the use of training parameters.
1: 2: |
|
DM : 14 x 506
0.00632 0.0273 0.0273 0.0324 0.0691 0.0299 0.0883 0.145 0.211 0.17 0.225 0.117 0.0938 0.63 0.638 0.627 1.05 0.784 0.803 0.726 1.25 0.852 1.23 0.988 0.75 0.841 0.672 0.956 0.773 1 1.13 1.35 1.39 1.15 1.61 0.0642 0.0974 0.0801 0.175 0.0276 0.0336 0.127 0.142 0.159 0.123 0.171 0.188 0.229 0.254 0.22 0.0887 0.0434 0.0536 0.0498 0.0136 0.0131 0.0206 0.0143 0.154 0.103 0.149 0.172 0.11 0.127 0.0195 0.0358 0.0438 0.0579 0.136 0.128 0.0883 0.159 0.0916 0.195 0.079 0.0951 0.102 0.0871 0.0565 0.0839 0.0411 0.0446 0.0366 0.0355 0.0506 0.0574 0.0519 0.0715 0.0566 0.053 0.0468 0.0393 0.042 0.0288 0.0429 0.122 0.115 0.121 0.0819 0.0686 0.149 0.114 0.229 0.212 0.14 0.133 0.171 0.131 0.128 0.264 0.108 0.101 0.123 0.222 0.142 0.171 0.132 0.151 0.131 0.145 0.069 0.0717 0.093 0.15 0.0985 0.169 0.387 0.259 0.325 0.881 0.34 1.19 0.59 0.33 0.976 0.558 0.323 0.352 0.25 0.545 0.291 1.63 3.32 4.1 2.78 2.38 2.16 2.37 2.33 2.73 1.66 1.5 1.13 2.15 1.41 3.54 2.45 1.22 1.34 1.43 1.27 1.46 1.83 1.52 2.24 2.92 2.01 1.8 2.3 2.45 1.21 2.31 0.139 0.0918 0.0845 0.0666 0.0702 0.0543 0.0664 0.0578 0.0659 0.0689 0.091 0.1 0.0831 0.0605 0.056 0.0788 0.126 0.0837 0.0907 0.0691 0.0866 0.0219 0.0144 0.0138 0.0401 0.0467 0.0377 0.0315 0.0178 0.0345 0.0218 0.0351 0.0201 0.136 0.23 0.252 0.136 0.436 0.174 0.376 0.217 0.141 0.29 0.198 0.0456 0.0701 0.111 0.114 0.358 0.408 0.624 0.615 0.315 0.527 0.382 0.412 0.298 0.442 0.537 0.463 0.575 0.331 0.448 0.33 0.521 0.512 0.0824 0.0925 0.113 0.106 0.103 0.128 0.206 0.191 0.34 0.197 0.164 0.191 0.14 0.214 0.0822 0.369 0.0482 0.0355 0.0154 0.612 0.664 0.657 0.54 0.534 0.52 0.825 0.55 0.762 0.786 0.578 0.541 0.0907 0.299 0.162 0.115 0.222 0.0564 0.096 0.105 0.0613 0.0798 0.21 0.0358 0.0371 0.0613 0.015 0.00906 0.011 0.0197 0.0387 0.0459 0.043 0.035 0.0789 0.0362 0.0827 0.082 0.129 0.0537 0.141 0.0647 0.0556 0.0442 0.0354 0.0927 0.1 0.0552 0.0548 0.075 0.0493 0.493 0.349 2.64 0.79 0.262 0.269 0.369 0.254 0.318 0.245 0.402 0.475 0.168 0.182 0.351 0.284 0.341 0.192 0.303 0.241 0.0662 0.0672 0.0454 0.0502 0.0347 0.0508 0.0374 0.0396 0.0343 0.0304 0.0331 0.055 0.0615 0.013 0.025 0.0254 0.0305 0.0311 0.0616 0.0187 0.015 0.029 0.0621 0.0795 0.0724 0.0171 0.043 0.107 8.98 3.85 5.2 4.26 4.54 3.84 3.68 4.22 3.47 4.56 3.7 3.52 4.9 5.67 6.54 9.23 8.27 1.11 8.5 9.61 5.29 9.82 3.65 7.87 8.98 5.87 9.19 7.99 0.0849 6.81 4.39 2.6 4.33 8.15 6.96 5.29 1.58 8.64 3.36 8.72 5.87 7.67 8.35 9.92 5.05 4.24 9.6 4.8 1.53 7.92 0.716 1.95 7.4 4.44 1.14 4.05 8.81 8.66 5.75 8.08 0.834 5.94 3.53 1.81 1.09 7.02 2.05 7.05 8.79 5.86 2.25 7.66 7.37 9.34 8.49 0.0623 6.44 5.58 3.91 1.16 4.42 5.18 3.68 9.39 2.05 9.72 5.67 9.97 2.8 0.672 6.29 9.92 9.33 7.53 6.72 5.44 5.09 8.25 9.51 4.75 4.67 8.2 7.75 6.8 4.81 3.69 6.65 5.82 7.84 3.16 3.77 4.42 5.58 3.08 4.35 4.04 3.57 4.65 8.06 6.39 4.87 5.02 0.233 4.33 5.82 5.71 5.73 2.82 2.38 3.67 5.69 4.84 0.151 0.183 0.207 0.106 0.111 0.173 0.28 0.179 0.29 0.268 0.239 0.178 0.224 0.0626 0.0453 0.0608 0.11 0.0474
18 0 0 0 0 0 12.5 12.5 12.5 12.5 12.5 12.5 12.5 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 75 75 0 0 0 0 0 0 0 0 0 21 21 21 21 75 90 85 100 25 25 25 25 25 25 17.5 80 80 12.5 12.5 12.5 0 0 0 0 0 0 0 0 0 0 25 25 25 25 0 0 0 0 0 0 0 0 28 28 28 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 45 45 45 45 45 45 60 60 80 80 80 80 95 95 82.5 82.5 95 95 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 30 30 30 30 30 30 22 22 22 22 22 22 22 22 22 22 80 80 90 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 40 40 40 40 40 20 20 20 20 90 90 55 80 52.5 52.5 52.5 80 80 80 0 0 0 0 0 70 70 70 34 34 34 33 33 33 33 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 35 35 0 0 0 0 0 0 0 0 35 0 55 55 0 0 85 80 40 40 60 60 90 80 80 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
2.31 7.07 7.07 2.18 2.18 2.18 7.87 7.87 7.87 7.87 7.87 7.87 7.87 8.14 8.14 8.14 8.14 8.14 8.14 8.14 8.14 8.14 8.14 8.14 8.14 8.14 8.14 8.14 8.14 8.14 8.14 8.14 8.14 8.14 8.14 5.96 5.96 5.96 5.96 2.95 2.95 6.91 6.91 6.91 6.91 6.91 6.91 6.91 6.91 6.91 5.64 5.64 5.64 5.64 4 1.22 0.74 1.32 5.13 5.13 5.13 5.13 5.13 5.13 1.38 3.37 3.37 6.07 6.07 6.07 10.8 10.8 10.8 10.8 12.8 12.8 12.8 12.8 12.8 12.8 4.86 4.86 4.86 4.86 4.49 4.49 4.49 4.49 3.41 3.41 3.41 3.41 15 15 15 2.89 2.89 2.89 2.89 2.89 8.56 8.56 8.56 8.56 8.56 8.56 8.56 8.56 8.56 8.56 8.56 10 10 10 10 10 10 10 10 10 25.7 25.7 25.7 25.7 25.7 25.7 25.7 21.9 21.9 21.9 21.9 21.9 21.9 21.9 21.9 21.9 21.9 21.9 21.9 21.9 21.9 21.9 19.6 19.6 19.6 19.6 19.6 19.6 19.6 19.6 19.6 19.6 19.6 19.6 19.6 19.6 19.6 19.6 19.6 19.6 19.6 19.6 19.6 19.6 19.6 19.6 19.6 19.6 19.6 19.6 19.6 19.6 4.05 4.05 4.05 4.05 4.05 4.05 4.05 2.46 2.46 2.46 2.46 2.46 2.46 2.46 2.46 3.44 3.44 3.44 3.44 3.44 3.44 2.93 2.93 0.46 1.52 1.52 1.52 1.47 1.47 2.03 2.03 2.68 2.68 10.6 10.6 10.6 10.6 10.6 10.6 10.6 10.6 10.6 10.6 10.6 13.9 13.9 13.9 13.9 6.2 6.2 6.2 6.2 6.2 6.2 6.2 6.2 6.2 6.2 6.2 6.2 6.2 6.2 6.2 6.2 6.2 6.2 4.93 4.93 4.93 4.93 4.93 4.93 5.86 5.86 5.86 5.86 5.86 5.86 5.86 5.86 5.86 5.86 3.64 3.64 3.75 3.97 3.97 3.97 3.97 3.97 3.97 3.97 3.97 3.97 3.97 3.97 3.97 6.96 6.96 6.96 6.96 6.96 6.41 6.41 6.41 6.41 6.41 3.33 3.33 3.33 3.33 1.21 2.97 2.25 1.76 5.32 5.32 5.32 4.95 4.95 4.95 13.9 13.9 13.9 13.9 13.9 2.24 2.24 2.24 6.09 6.09 6.09 2.18 2.18 2.18 2.18 9.9 9.9 9.9 9.9 9.9 9.9 9.9 9.9 9.9 9.9 9.9 9.9 7.38 7.38 7.38 7.38 7.38 7.38 7.38 7.38 3.24 3.24 3.24 6.06 6.06 5.19 5.19 5.19 5.19 5.19 5.19 5.19 5.19 1.52 1.89 3.78 3.78 4.39 4.39 4.15 2.01 1.25 1.25 1.69 1.69 2.02 1.91 1.91 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 18.1 27.7 27.7 27.7 27.7 27.7 9.69 9.69 9.69 9.69 9.69 9.69 9.69 9.69 11.9 11.9 11.9 11.9 11.9
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 1 1 0 0 0 0 1 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 1 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 1 0 1 1 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 1 1 0 0 0 0 1 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0.538 0.469 0.469 0.458 0.458 0.458 0.524 0.524 0.524 0.524 0.524 0.524 0.524 0.538 0.538 0.538 0.538 0.538 0.538 0.538 0.538 0.538 0.538 0.538 0.538 0.538 0.538 0.538 0.538 0.538 0.538 0.538 0.538 0.538 0.538 0.499 0.499 0.499 0.499 0.428 0.428 0.448 0.448 0.448 0.448 0.448 0.448 0.448 0.448 0.448 0.439 0.439 0.439 0.439 0.41 0.403 0.41 0.411 0.453 0.453 0.453 0.453 0.453 0.453 0.416 0.398 0.398 0.409 0.409 0.409 0.413 0.413 0.413 0.413 0.437 0.437 0.437 0.437 0.437 0.437 0.426 0.426 0.426 0.426 0.449 0.449 0.449 0.449 0.489 0.489 0.489 0.489 0.464 0.464 0.464 0.445 0.445 0.445 0.445 0.445 0.52 0.52 0.52 0.52 0.52 0.52 0.52 0.52 0.52 0.52 0.52 0.547 0.547 0.547 0.547 0.547 0.547 0.547 0.547 0.547 0.581 0.581 0.581 0.581 0.581 0.581 0.581 0.624 0.624 0.624 0.624 0.624 0.624 0.624 0.624 0.624 0.624 0.624 0.624 0.624 0.624 0.624 0.871 0.871 0.871 0.871 0.871 0.871 0.871 0.871 0.871 0.871 0.871 0.871 0.871 0.871 0.871 0.605 0.605 0.871 0.605 0.605 0.605 0.605 0.605 0.605 0.605 0.605 0.605 0.605 0.605 0.605 0.51 0.51 0.51 0.51 0.51 0.51 0.51 0.488 0.488 0.488 0.488 0.488 0.488 0.488 0.488 0.437 0.437 0.437 0.437 0.437 0.437 0.401 0.401 0.422 0.404 0.404 0.404 0.403 0.403 0.415 0.415 0.416 0.416 0.489 0.489 0.489 0.489 0.489 0.489 0.489 0.489 0.489 0.489 0.489 0.55 0.55 0.55 0.55 0.507 0.507 0.507 0.507 0.504 0.504 0.504 0.504 0.504 0.504 0.504 0.504 0.507 0.507 0.507 0.507 0.507 0.507 0.428 0.428 0.428 0.428 0.428 0.428 0.431 0.431 0.431 0.431 0.431 0.431 0.431 0.431 0.431 0.431 0.392 0.392 0.394 0.647 0.647 0.647 0.647 0.647 0.647 0.647 0.647 0.647 0.647 0.575 0.575 0.464 0.464 0.464 0.464 0.464 0.447 0.447 0.447 0.447 0.447 0.443 0.443 0.443 0.443 0.401 0.4 0.389 0.385 0.405 0.405 0.405 0.411 0.411 0.411 0.437 0.437 0.437 0.437 0.437 0.4 0.4 0.4 0.433 0.433 0.433 0.472 0.472 0.472 0.472 0.544 0.544 0.544 0.544 0.544 0.544 0.544 0.544 0.544 0.544 0.544 0.544 0.493 0.493 0.493 0.493 0.493 0.493 0.493 0.493 0.46 0.46 0.46 0.438 0.438 0.515 0.515 0.515 0.515 0.515 0.515 0.515 0.515 0.442 0.518 0.484 0.484 0.442 0.442 0.429 0.435 0.429 0.429 0.411 0.411 0.41 0.413 0.413 0.77 0.77 0.77 0.77 0.77 0.77 0.77 0.77 0.718 0.718 0.718 0.631 0.631 0.631 0.631 0.631 0.668 0.668 0.668 0.671 0.671 0.671 0.671 0.671 0.671 0.671 0.7 0.7 0.7 0.7 0.7 0.7 0.7 0.7 0.7 0.7 0.7 0.693 0.693 0.693 0.693 0.693 0.693 0.693 0.693 0.693 0.693 0.693 0.693 0.693 0.659 0.659 0.597 0.597 0.597 0.597 0.597 0.597 0.693 0.679 0.679 0.679 0.679 0.718 0.718 0.718 0.614 0.614 0.584 0.679 0.584 0.679 0.679 0.679 0.584 0.584 0.584 0.713 0.713 0.74 0.74 0.74 0.74 0.74 0.74 0.74 0.74 0.74 0.74 0.74 0.74 0.74 0.713 0.713 0.713 0.713 0.713 0.713 0.713 0.713 0.713 0.713 0.713 0.713 0.713 0.713 0.713 0.713 0.655 0.655 0.655 0.584 0.58 0.58 0.58 0.532 0.58 0.614 0.584 0.584 0.614 0.614 0.614 0.614 0.532 0.532 0.532 0.532 0.583 0.583 0.583 0.583 0.609 0.609 0.609 0.609 0.609 0.585 0.585 0.585 0.585 0.585 0.585 0.585 0.585 0.573 0.573 0.573 0.573 0.573
6.58 6.42 7.19 7 7.15 6.43 6.01 6.17 5.63 6 6.38 6.01 5.89 5.95 6.1 5.83 5.94 5.99 5.46 5.73 5.57 5.97 6.14 5.81 5.92 5.6 5.81 6.05 6.5 6.67 5.71 6.07 5.95 5.7 6.1 5.93 5.84 5.85 5.97 6.6 7.02 6.77 6.17 6.21 6.07 5.68 5.79 6.03 5.4 5.6 5.96 6.12 6.51 6 5.89 7.25 6.38 6.82 6.15 5.93 5.74 5.97 6.46 6.76 7.1 6.29 5.79 5.88 5.59 5.89 6.42 5.96 6.07 6.25 6.27 6.29 6.28 6.14 6.23 5.87 6.73 6.62 6.3 6.17 6.39 6.63 6.02 6.12 7.01 7.08 6.42 6.41 6.44 6.21 6.25 6.63 6.16 8.07 7.82 7.42 6.73 6.78 6.41 6.14 6.17 5.85 5.84 6.13 6.47 6.23 6.2 6.72 5.91 6.09 6.25 5.93 6.18 6.02 5.87 5.73 5.87 6 5.96 5.86 5.88 5.99 5.61 5.69 6.43 5.64 6.46 6.33 6.37 5.82 5.76 6.34 5.94 6.45 5.86 6.15 6.17 5.02 5.4 5.47 4.9 6.13 5.63 4.93 5.19 5.6 6.12 5.4 5.01 5.71 6.13 6.15 5.27 6.94 6.07 6.51 6.25 7.49 7.8 8.38 5.85 6.1 7.93 5.88 6.32 6.4 5.88 5.88 5.57 6.42 5.86 6.55 6.02 6.32 6.86 6.98 7.77 6.14 7.16 6.56 5.6 6.15 7.83 6.78 6.56 7.19 6.95 6.74 7.18 6.8 6.6 7.88 7.29 7.11 7.27 6.98 7.14 6.16 7.61 7.85 8.03 5.89 6.33 5.78 6.06 5.34 5.96 5.4 5.81 6.38 5.41 6.18 5.89 6.64 5.95 6.37 6.95 6.16 6.88 6.62 8.27 8.73 8.04 7.16 7.69 6.55 5.98 7.41 8.34 8.25 6.73 6.09 6.63 7.36 6.48 6.61 6.9 6.1 6.36 6.39 5.59 5.61 6.11 6.23 6.43 6.72 6.49 6.44 6.96 8.26 6.11 5.88 7.45 8.7 7.33 6.84 7.2 7.52 8.4 7.33 7.21 5.56 7.01 8.3 7.47 5.92 5.86 6.24 6.54 7.69 6.76 6.85 7.27 6.83 6.48 6.81 7.82 6.97 7.65 7.92 7.09 6.45 6.23 6.21 6.32 6.57 6.86 7.15 6.63 6.13 6.01 6.68 6.55 5.79 6.35 7.04 6.87 6.59 6.5 6.98 7.24 6.62 7.42 6.85 6.64 5.97 4.97 6.12 6.02 6.27 6.57 5.71 5.91 5.78 6.38 6.11 6.43 6.38 6.04 5.71 6.42 6.43 6.31 6.08 5.87 6.33 6.14 5.71 6.03 6.32 6.31 6.04 5.87 5.9 6.06 5.99 5.97 7.24 6.54 6.7 6.87 6.01 5.9 6.52 6.64 6.94 6.49 6.58 5.88 6.73 5.66 5.94 6.21 6.4 6.13 6.11 6.4 6.25 5.36 5.8 8.78 3.56 4.96 3.86 4.97 6.68 7.02 6.22 5.88 4.91 4.14 7.31 6.65 6.79 6.38 6.22 6.97 6.55 5.54 5.52 4.37 5.28 4.65 5 4.88 5.39 5.71 6.05 5.04 6.19 5.89 6.47 6.41 5.75 5.45 5.85 5.99 6.34 6.4 5.35 5.53 5.68 4.14 5.61 5.62 6.85 5.76 6.66 4.63 5.16 4.52 6.43 6.78 5.3 5.96 6.82 6.41 6.01 5.65 6.1 5.57 5.9 5.84 6.2 6.19 6.38 6.35 6.83 6.43 6.44 6.21 6.63 6.46 6.15 5.94 5.63 5.82 6.41 6.22 6.49 5.85 6.46 6.34 6.25 6.19 6.42 6.75 6.66 6.3 7.39 6.73 6.53 5.98 5.94 6.3 6.08 6.7 6.38 6.32 6.51 6.21 5.76 5.95 6 5.93 5.71 6.17 6.23 6.44 6.98 5.43 6.16 6.48 5.3 6.19 6.23 6.24 6.75 7.06 5.76 5.87 6.31 6.11 5.91 5.45 5.41 5.09 5.98 5.98 5.71 5.93 5.67 5.39 5.79 6.02 5.57 6.03 6.59 6.12 6.98 6.79 6.03
65.2 78.9 61.1 45.8 54.2 58.7 66.6 96.1 100 85.9 94.3 82.9 39 61.8 84.5 56.5 29.3 81.7 36.6 69.5 98.1 89.2 91.7 100 94.1 85.7 90.3 88.8 94.4 87.3 94.1 100 82 95 96.9 68.2 61.4 41.5 30.2 21.8 15.8 2.9 6.6 6.5 40 33.8 33.3 85.5 95.3 62 45.7 63 21.1 21.4 47.6 21.9 35.7 40.5 29.2 47.2 66.2 93.4 67.8 43.4 59.5 17.8 31.1 21.4 36.8 33 6.6 17.5 7.8 6.2 6 45 74.5 45.8 53.7 36.6 33.5 70.4 32.2 46.7 48 56.1 45.1 56.8 86.3 63.1 66.1 73.9 53.6 28.9 77.3 57.8 69.6 76 36.9 62.5 79.9 71.3 85.4 87.4 90 96.7 91.9 85.2 97.1 91.2 54.4 81.6 92.9 95.4 84.2 88.2 72.5 82.6 73.1 65.2 69.7 84.1 92.9 97 95.8 88.4 95.6 96 98.8 94.7 98.9 97.7 97.9 95.4 98.4 98.2 93.5 98.4 98.2 97.9 93.6 100 100 100 97.8 100 100 95.7 93.8 94.9 97.3 100 88 98.5 96 82.6 94 97.4 100 100 92.6 90.8 98.2 93.9 91.8 93 96.2 79.2 96.1 95.2 94.6 97.3 88.5 84.1 68.7 33.1 47.2 73.4 74.4 58.4 83.3 62.2 92.2 95.6 89.8 68.8 53.6 41.1 29.1 38.9 21.5 30.8 26.3 9.9 18.8 32 34.1 36.6 38.3 15.3 13.9 38.4 15.7 33.2 31.9 22.3 52.5 72.7 59.1 100 92.1 88.6 53.8 32.3 9.8 42.4 56 85.1 93.8 92.4 88.5 91.3 77.7 80.8 78.3 83 86.5 79.9 17 21.4 68.1 76.9 73.3 70.4 66.5 61.5 76.5 71.6 18.5 42.2 54.3 65.1 52.9 7.8 76.5 70.2 34.9 79.2 49.1 17.5 13 8.9 6.8 8.4 32 19.1 34.2 86.9 100 100 81.8 89.4 91.5 94.5 91.6 62.8 84.6 67 52.6 61.5 42.1 16.3 58.7 51.8 32.9 42.8 49 27.6 32.1 32.2 64.5 37.2 49.7 24.8 20.8 31.9 31.5 31.3 45.6 22.9 27.9 27.7 23.4 18.4 42.3 31.1 51 58 20.1 10 47.4 40.4 18.4 17.7 41.1 58.1 71.9 70.3 82.5 76.7 37.8 52.8 90.4 82.8 87.3 77.7 83.2 71.7 67.2 58.8 52.3 54.3 49.9 74.3 40.1 14.7 28.9 43.7 25.8 17.2 32.2 28.4 23.3 38.1 38.5 34.5 46.3 59.6 37.3 45.4 58.5 49.3 59.7 56.4 28.1 48.5 52.3 27.7 29.7 34.5 44.4 35.9 18.5 36.1 21.9 19.5 97.4 91 83.4 81.3 88 91.1 96.2 89 82.9 87.9 91.4 100 100 96.8 97.5 100 89.6 100 100 97.9 93.3 98.8 96.2 100 91.9 99.1 100 100 91.2 98.1 100 89.5 100 98.9 97 82.5 97 92.6 94.7 98.8 96 98.9 100 77.8 100 100 100 96 85.4 100 100 100 97.9 100 100 100 100 100 100 100 90.8 89.1 100 76.5 100 95.3 87.6 85.1 70.6 95.4 59.7 78.7 78.1 95.6 86.1 94.3 74.8 87.9 95 94.6 93.3 100 87.9 93.9 92.4 97.2 100 100 96.6 94.8 96.4 96.6 98.7 98.3 92.6 98.2 91.8 99.3 94.1 86.5 87.9 80.3 83.7 84.4 90 88.4 83 89.9 65.4 48.2 84.7 94.5 71 56.7 84 90.7 75 67.6 95.4 97.4 93.6 97.3 96.7 88 64.7 74.9 77 40.3 41.9 51.9 79.8 53.2 92.7 98.3 98 98.8 83.5 54 42.6 28.8 72.9 70.6 65.3 73.5 79.7 69.1 76.7 91 89.3 80.8
4.09 4.97 4.97 6.06 6.06 6.06 5.56 5.95 6.08 6.59 6.35 6.23 5.45 4.71 4.46 4.5 4.5 4.26 3.8 3.8 3.8 4.01 3.98 4.1 4.4 4.45 4.68 4.45 4.45 4.24 4.23 4.18 3.99 3.79 3.76 3.36 3.38 3.93 3.85 5.4 5.4 5.72 5.72 5.72 5.72 5.1 5.1 5.69 5.87 6.09 6.81 6.81 6.81 6.81 7.32 8.7 9.19 8.32 7.81 6.93 7.23 6.82 7.23 7.98 9.22 6.61 6.61 6.5 6.5 6.5 5.29 5.29 5.29 5.29 4.25 4.5 4.05 4.09 5.01 4.5 5.4 5.4 5.4 5.4 4.78 4.44 4.43 3.75 3.42 3.41 3.09 3.09 3.67 3.67 3.62 3.5 3.5 3.5 3.5 3.5 2.78 2.86 2.71 2.71 2.42 2.11 2.21 2.12 2.43 2.55 2.78 2.68 2.35 2.55 2.26 2.46 2.73 2.75 2.48 2.76 2.26 2.2 2.09 1.94 2.01 1.99 1.76 1.79 1.81 1.98 2.12 2.27 2.33 2.47 2.35 2.11 1.97 1.85 1.67 1.67 1.61 1.44 1.32 1.41 1.35 1.42 1.52 1.46 1.53 1.53 1.62 1.59 1.61 1.62 1.75 1.75 1.74 1.88 1.76 1.77 1.8 1.97 2.04 2.16 2.42 2.28 2.05 2.43 2.1 2.26 2.43 2.39 2.6 2.65 2.7 3.13 3.55 3.32 2.92 2.83 2.74 2.6 2.7 2.85 2.99 3.28 3.2 3.79 4.57 4.57 6.48 6.48 6.48 6.22 6.22 5.65 7.31 7.31 7.31 7.65 7.65 6.27 6.27 5.12 5.12 3.95 4.35 4.35 4.24 3.88 3.88 3.67 3.65 3.95 3.59 3.95 3.11 3.42 2.89 3.36 2.86 3.05 3.27 3.27 2.89 2.89 3.22 3.22 3.38 3.38 3.67 3.67 3.84 3.65 3.65 3.65 4.15 4.15 6.19 6.19 6.34 6.34 7.04 7.04 7.95 7.95 8.06 8.06 7.83 7.83 7.4 7.4 8.91 8.91 9.22 9.22 6.34 1.8 1.89 2.01 2.11 2.14 2.29 2.08 1.93 1.99 2.13 2.42 2.87 3.92 4.43 4.43 3.92 4.37 4.08 4.27 4.79 4.86 4.14 4.1 4.69 5.24 5.21 5.89 7.31 7.31 9.09 7.32 7.32 7.32 5.12 5.12 5.12 5.5 5.5 5.96 5.96 6.32 7.83 7.83 7.83 5.49 5.49 5.49 4.02 3.37 3.1 3.18 3.32 3.1 2.52 2.64 2.83 3.26 3.6 3.95 4 4.03 3.53 4 4.54 4.54 4.72 4.72 4.72 5.42 5.42 5.42 5.21 5.21 5.87 6.64 6.64 6.46 6.46 5.99 5.23 5.62 4.81 4.81 4.81 7.04 6.27 5.73 6.47 8.01 8.01 8.54 8.34 8.79 8.79 10.7 10.7 12.1 10.6 10.6 2.12 2.51 2.72 2.51 2.52 2.3 2.1 1.9 1.9 1.61 1.75 1.51 1.33 1.36 1.2 1.17 1.13 1.17 1.14 1.32 1.34 1.36 1.39 1.39 1.42 1.52 1.58 1.53 1.44 1.43 1.47 1.52 1.59 1.73 1.93 2.17 1.77 1.79 1.78 1.73 1.68 1.63 1.49 1.5 1.59 1.57 1.64 1.7 1.61 1.43 1.18 1.29 1.45 1.47 1.41 1.53 1.55 1.59 1.66 1.83 1.82 1.65 1.8 1.79 1.86 1.87 1.95 2.02 2.06 1.91 2 1.86 1.94 1.97 2.05 2.09 2.2 2.32 2.22 2.12 2 1.91 1.82 1.82 1.87 2.07 2 1.98 1.9 1.99 2.07 2.2 2.26 2.19 2.32 2.36 2.37 2.45 2.5 2.44 2.58 2.78 2.78 2.72 2.6 2.57 2.73 2.8 2.96 3.07 2.87 2.54 2.91 2.82 3.03 3.1 2.9 2.53 2.43 2.21 2.31 2.1 2.17 1.95 3.42 3.33 3.41 4.1 3.72 3.99 3.55 3.15 1.82 1.76 1.82 1.87 2.11 2.38 2.38 2.8 2.8 2.89 2.41 2.4 2.5 2.48 2.29 2.17 2.39 2.51
1 2 2 3 3 3 5 5 5 5 5 5 5 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 5 5 5 5 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 3 5 2 5 8 8 8 8 8 8 3 4 4 4 4 4 4 4 4 4 5 5 5 5 5 5 4 4 4 4 3 3 3 3 2 2 2 2 4 4 4 2 2 2 2 2 5 5 5 5 5 5 5 5 5 5 5 6 6 6 6 6 6 6 6 6 2 2 2 2 2 2 2 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 3 3 3 3 3 3 3 3 5 5 5 5 5 5 1 1 4 2 2 2 3 3 2 2 4 4 4 4 4 4 4 4 4 4 4 4 4 5 5 5 5 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 6 6 6 6 6 6 7 7 7 7 7 7 7 7 7 7 1 1 3 5 5 5 5 5 5 5 5 5 5 5 5 3 3 3 3 3 4 4 4 4 4 5 5 5 5 1 1 1 1 6 6 6 4 4 4 4 4 4 4 4 5 5 5 7 7 7 7 7 7 7 4 4 4 4 4 4 4 4 4 4 4 4 5 5 5 5 5 5 5 5 4 4 4 1 1 5 5 5 5 5 5 5 5 1 1 5 5 3 3 4 4 1 1 4 4 5 4 4 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 4 4 4 4 4 6 6 6 6 6 6 6 6 1 1 1 1 1
296 242 242 222 222 222 311 311 311 311 311 311 311 307 307 307 307 307 307 307 307 307 307 307 307 307 307 307 307 307 307 307 307 307 307 279 279 279 279 252 252 233 233 233 233 233 233 233 233 233 243 243 243 243 469 226 313 256 284 284 284 284 284 284 216 337 337 345 345 345 305 305 305 305 398 398 398 398 398 398 281 281 281 281 247 247 247 247 270 270 270 270 270 270 270 276 276 276 276 276 384 384 384 384 384 384 384 384 384 384 384 432 432 432 432 432 432 432 432 432 188 188 188 188 188 188 188 437 437 437 437 437 437 437 437 437 437 437 437 437 437 437 403 403 403 403 403 403 403 403 403 403 403 403 403 403 403 403 403 403 403 403 403 403 403 403 403 403 403 403 403 403 296 296 296 296 296 296 296 193 193 193 193 193 193 193 193 398 398 398 398 398 398 265 265 255 329 329 329 402 402 348 348 224 224 277 277 277 277 277 277 277 277 277 277 277 276 276 276 276 307 307 307 307 307 307 307 307 307 307 307 307 307 307 307 307 307 307 300 300 300 300 300 300 330 330 330 330 330 330 330 330 330 330 315 315 244 264 264 264 264 264 264 264 264 264 264 264 264 223 223 223 223 223 254 254 254 254 254 216 216 216 216 198 285 300 241 293 293 293 245 245 245 289 289 289 289 289 358 358 358 329 329 329 222 222 222 222 304 304 304 304 304 304 304 304 304 304 304 304 287 287 287 287 287 287 287 287 430 430 430 304 304 224 224 224 224 224 224 224 224 284 422 370 370 352 352 351 280 335 335 411 411 187 334 334 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 666 711 711 711 711 711 391 391 391 391 391 391 391 391 273 273 273 273 273
15.3 17.8 17.8 18.7 18.7 18.7 15.2 15.2 15.2 15.2 15.2 15.2 15.2 21 21 21 21 21 21 21 21 21 21 21 21 21 21 21 21 21 21 21 21 21 21 19.2 19.2 19.2 19.2 18.3 18.3 17.9 17.9 17.9 17.9 17.9 17.9 17.9 17.9 17.9 16.8 16.8 16.8 16.8 21.1 17.9 17.3 15.1 19.7 19.7 19.7 19.7 19.7 19.7 18.6 16.1 16.1 18.9 18.9 18.9 19.2 19.2 19.2 19.2 18.7 18.7 18.7 18.7 18.7 18.7 19 19 19 19 18.5 18.5 18.5 18.5 17.8 17.8 17.8 17.8 18.2 18.2 18.2 18 18 18 18 18 20.9 20.9 20.9 20.9 20.9 20.9 20.9 20.9 20.9 20.9 20.9 17.8 17.8 17.8 17.8 17.8 17.8 17.8 17.8 17.8 19.1 19.1 19.1 19.1 19.1 19.1 19.1 21.2 21.2 21.2 21.2 21.2 21.2 21.2 21.2 21.2 21.2 21.2 21.2 21.2 21.2 21.2 14.7 14.7 14.7 14.7 14.7 14.7 14.7 14.7 14.7 14.7 14.7 14.7 14.7 14.7 14.7 14.7 14.7 14.7 14.7 14.7 14.7 14.7 14.7 14.7 14.7 14.7 14.7 14.7 14.7 14.7 16.6 16.6 16.6 16.6 16.6 16.6 16.6 17.8 17.8 17.8 17.8 17.8 17.8 17.8 17.8 15.2 15.2 15.2 15.2 15.2 15.2 15.6 15.6 14.4 12.6 12.6 12.6 17 17 14.7 14.7 14.7 14.7 18.6 18.6 18.6 18.6 18.6 18.6 18.6 18.6 18.6 18.6 18.6 16.4 16.4 16.4 16.4 17.4 17.4 17.4 17.4 17.4 17.4 17.4 17.4 17.4 17.4 17.4 17.4 17.4 17.4 17.4 17.4 17.4 17.4 16.6 16.6 16.6 16.6 16.6 16.6 19.1 19.1 19.1 19.1 19.1 19.1 19.1 19.1 19.1 19.1 16.4 16.4 15.9 13 13 13 13 13 13 13 13 13 13 13 13 18.6 18.6 18.6 18.6 18.6 17.6 17.6 17.6 17.6 17.6 14.9 14.9 14.9 14.9 13.6 15.3 15.3 18.2 16.6 16.6 16.6 19.2 19.2 19.2 16 16 16 16 16 14.8 14.8 14.8 16.1 16.1 16.1 18.4 18.4 18.4 18.4 18.4 18.4 18.4 18.4 18.4 18.4 18.4 18.4 18.4 18.4 18.4 18.4 19.6 19.6 19.6 19.6 19.6 19.6 19.6 19.6 16.9 16.9 16.9 16.9 16.9 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 15.5 15.9 17.6 17.6 18.8 18.8 17.9 17 19.7 19.7 18.3 18.3 17 22 22 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.2 20.1 20.1 20.1 20.1 20.1 19.2 19.2 19.2 19.2 19.2 19.2 19.2 19.2 21 21 21 21 21
397 397 393 395 397 394 396 397 387 387 393 397 391 397 380 396 387 387 289 391 377 393 397 395 394 303 377 306 388 380 360 377 233 359 248 397 378 397 393 396 396 385 383 394 389 397 397 393 397 397 396 394 397 397 397 396 397 393 391 397 395 378 397 396 393 397 397 396 397 397 384 377 391 377 395 383 374 387 386 396 397 396 397 391 397 392 396 395 397 396 392 394 395 396 397 358 392 397 394 397 395 396 70.8 394 393 394 396 388 395 391 393 396 395 397 389 345 393 395 339 392 389 378 378 370 379 385 359 392 397 397 395 397 386 389 263 395 378 394 392 397 388 397 397 397 397 173 169 392 357 352 373 342 343 262 321 88 88.6 363 354 364 339 374 390 388 395 240 369 228 297 330 292 348 397 396 393 391 393 396 391 397 396 397 394 397 391 387 393 394 383 397 378 390 390 393 377 394 397 354 392 397 384 394 395 393 391 397 395 389 381 397 393 395 391 386 349 394 393 393 397 394 392 395 390 397 385 382 387 372 378 380 378 376 386 379 360 377 388 390 379 384 391 395 373 375 372 389 390 376 375 394 396 377 386 397 393 395 386 390 383 392 393 388 387 393 388 392 384 385 390 391 389 397 395 391 397 397 389 393 397 397 387 392 377 396 395 395 342 397 397 372 397 397 397 397 397 397 393 397 368 372 391 396 384 390 394 393 397 397 397 396 350 397 396 393 396 396 391 397 395 396 397 397 397 391 397 394 397 397 382 375 369 394 362 390 389 397 397 395 396 397 397 395 390 397 388 386 365 392 391 390 397 371 392 384 383 376 378 391 395 391 375 351 381 353 355 355 316 131 376 375 392 366 348 397 397 397 363 397 397 394 397 397 397 397 286 397 397 397 373 397 394 378 397 397 397 392 397 393 397 338 397 397 376 397 329 385 370 332 315 179 2.6 35.1 28.8 211 88.3 27.3 21.6 127 16.5 48.5 319 320 292 2.52 3.65 7.68 24.7 18.8 96.7 60.7 83.5 81.3 98 100 101 110 27.5 9.32 69 397 391 386 396 387 241 43.1 318 389 397 304 0.32 355 385 376 6.68 50.9 10.5 3.5 272 397 255 391 397 394 397 334 22 331 369 397 397 395 393 375 353 303 396 349 380 383 397 393 395 393 371 389 393 388 395 344 318 390 397 397 397 393 397 397 397 396 397 392 397 397 393 397
4.98 9.14 4.03 2.94 5.33 5.21 12.4 19.2 29.9 17.1 20.5 13.3 15.7 8.26 10.3 8.47 6.58 14.7 11.7 11.3 21 13.8 18.7 19.9 16.3 16.5 14.8 17.3 12.8 12 22.6 13 27.7 18.4 20.3 9.68 11.4 8.77 10.1 4.32 1.98 4.84 5.81 7.44 9.55 10.2 14.2 18.8 30.8 16.2 13.5 9.43 5.28 8.43 14.8 4.81 5.77 3.95 6.86 9.22 13.2 14.4 6.73 9.5 8.05 4.67 10.2 8.1 13.1 8.79 6.72 9.88 5.52 7.54 6.78 8.94 12 10.3 12.3 9.1 5.29 7.22 6.72 7.51 9.62 6.53 12.9 8.44 5.5 5.7 8.81 8.2 8.16 6.21 10.6 6.65 11.3 4.21 3.57 6.19 9.42 7.67 10.6 13.4 12.3 16.5 18.7 14.1 12.3 15.6 13 10.2 16.2 17.1 10.5 15.8 12 10.3 15.4 13.6 14.4 14.3 17.9 25.4 17.6 14.8 27.3 17.2 15.4 18.3 12.6 12.3 11.1 15 17.3 17 16.9 14.6 21.3 18.5 24.2 34.4 26.8 26.4 29.3 27.8 16.7 29.5 28.3 21.5 14.1 13.3 12.1 15.8 15.1 15 16.1 4.59 6.43 7.39 5.5 1.73 1.92 3.32 11.6 9.81 3.7 12.1 11.1 11.3 14.4 12 14.7 9.04 9.64 5.33 10.1 6.29 6.92 5.04 7.56 9.45 4.82 5.68 14 13.2 4.45 6.68 4.56 5.39 5.1 4.69 2.87 5.03 4.38 2.97 4.08 8.61 6.62 4.56 4.45 7.43 3.11 3.81 2.88 10.9 11 18.1 14.7 23.1 17.3 24 16 9.38 29.6 9.47 13.5 9.69 17.9 10.5 9.71 21.5 9.93 7.6 4.14 4.63 3.13 6.36 3.92 3.76 11.7 5.25 2.47 3.95 8.05 10.9 9.54 4.73 6.36 7.37 11.4 12.4 11.2 5.19 12.5 18.5 9.16 10.2 9.52 6.56 5.9 3.59 3.53 3.54 6.57 9.25 3.11 5.12 7.79 6.9 9.59 7.26 5.91 11.3 8.1 10.5 14.8 7.44 3.16 13.7 13 6.59 7.73 6.58 3.53 2.98 6.05 4.16 7.19 4.85 3.76 4.59 3.01 3.16 7.85 8.23 12.9 7.14 7.6 9.51 3.33 3.56 4.7 8.58 10.4 6.27 7.39 15.8 4.97 4.74 6.07 9.5 8.67 4.86 6.93 8.93 6.47 7.53 4.54 9.97 12.6 5.98 11.7 7.9 9.28 11.5 18.3 15.9 10.4 12.7 7.2 6.87 7.7 11.7 6.12 5.08 6.15 12.8 9.97 7.34 9.09 12.4 7.83 5.68 6.75 8.01 9.8 10.6 8.51 9.74 9.29 5.49 8.65 7.18 4.61 10.5 12.7 6.36 5.99 5.89 5.98 5.49 7.79 4.5 8.05 5.57 17.6 13.3 11.5 12.7 7.79 14.2 10.2 14.6 5.29 7.12 14 13.3 3.26 3.73 2.96 9.53 8.88 34.8 38 13.4 23.2 21.2 23.7 21.8 17.2 21.1 23.6 24.6 30.6 30.8 28.3 32 30.6 20.9 17.1 18.8 25.7 15.2 16.4 17.1 19.4 19.9 30.6 30 26.8 20.3 20.3 19.8 27.4 23 23.3 12.1 26.4 19.8 10.1 21.2 34.4 20.1 37 29.1 25.8 26.6 20.6 22.7 15 15.7 14.1 23.3 17.2 24.4 15.7 14.5 21.5 24.1 17.6 19.7 12 16.2 15.2 23.3 18.1 26.5 34 22.9 22.1 19.5 16.6 18.9 23.8 24 17.8 16.4 18.1 19.3 17.4 17.7 17.3 16.7 18.7 18.1 19 16.9 16.2 14.7 16.4 14.7 14 10.3 13.2 14.1 17.2 21.3 18.1 14.8 16.3 12.9 14.4 11.7 18.1 24.1 18.7 24.9 18 13.1 10.7 7.74 7.01 10.4 13.3 10.6 15 11.5 18.1 24 29.7 18.1 13.4 12 13.6 17.6 21.1 14.1 12.9 15.1 14.3 9.67 9.08 5.64 6.48 7.88
24 21.6 34.7 33.4 36.2 28.7 22.9 27.1 16.5 18.9 15 18.9 21.7 20.4 18.2 19.9 23.1 17.5 20.2 18.2 13.6 19.6 15.2 14.5 15.6 13.9 16.6 14.8 18.4 21 12.7 14.5 13.2 13.1 13.5 18.9 20 21 24.7 30.8 34.9 26.6 25.3 24.7 21.2 19.3 20 16.6 14.4 19.4 19.7 20.5 25 23.4 18.9 35.4 24.7 31.6 23.3 19.6 18.7 16 22.2 25 33 23.5 19.4 22 17.4 20.9 24.2 21.7 22.8 23.4 24.1 21.4 20 20.8 21.2 20.3 28 23.9 24.8 22.9 23.9 26.6 22.5 22.2 23.6 28.7 22.6 22 22.9 25 20.6 28.4 21.4 38.7 43.8 33.2 27.5 26.5 18.6 19.3 20.1 19.5 19.5 20.4 19.8 19.4 21.7 22.8 18.8 18.7 18.5 18.3 21.2 19.2 20.4 19.3 22 20.3 20.5 17.3 18.8 21.4 15.7 16.2 18 14.3 19.2 19.6 23 18.4 15.6 18.1 17.4 17.1 13.3 17.8 14 14.4 13.4 15.6 11.8 13.8 15.6 14.6 17.8 15.4 21.5 19.6 15.3 19.4 17 15.6 13.1 41.3 24.3 23.3 27 50 50 50 22.7 25 50 23.8 23.8 22.3 17.4 19.1 23.1 23.6 22.6 29.4 23.2 24.6 29.9 37.2 39.8 36.2 37.9 32.5 26.4 29.6 50 32 29.8 34.9 37 30.5 36.4 31.1 29.1 50 33.3 30.3 34.6 34.9 32.9 24.1 42.3 48.5 50 22.6 24.4 22.5 24.4 20 21.7 19.3 22.4 28.1 23.7 25 23.3 28.7 21.5 23 26.7 21.7 27.5 30.1 44.8 50 37.6 31.6 46.7 31.5 24.3 31.7 41.7 48.3 29 24 25.1 31.5 23.7 23.3 22 20.1 22.2 23.7 17.6 18.5 24.3 20.5 24.5 26.2 24.4 24.8 29.6 42.8 21.9 20.9 44 50 36 30.1 33.8 43.1 48.8 31 36.5 22.8 30.7 50 43.5 20.7 21.1 25.2 24.4 35.2 32.4 32 33.2 33.1 29.1 35.1 45.4 35.4 46 50 32.2 22 20.1 23.2 22.3 24.8 28.5 37.3 27.9 23.9 21.7 28.6 27.1 20.3 22.5 29 24.8 22 26.4 33.1 36.1 28.4 33.4 28.2 22.8 20.3 16.1 22.1 19.4 21.6 23.8 16.2 17.8 19.8 23.1 21 23.8 23.1 20.4 18.5 25 24.6 23 22.2 19.3 22.6 19.8 17.1 19.4 22.2 20.7 21.1 19.5 18.5 20.6 19 18.7 32.7 16.5 23.9 31.2 17.5 17.2 23.1 24.5 26.6 22.9 24.1 18.6 30.1 18.2 20.6 17.8 21.7 22.7 22.6 25 19.9 20.8 16.8 21.9 27.5 21.9 23.1 50 50 50 50 50 13.8 13.8 15 13.9 13.3 13.1 10.2 10.4 10.9 11.3 12.3 8.8 7.2 10.5 7.4 10.2 11.5 15.1 23.2 9.7 13.8 12.7 13.1 12.5 8.5 5 6.3 5.6 7.2 12.1 8.3 8.5 5 11.9 27.9 17.2 27.5 15 17.2 17.9 16.3 7 7.2 7.5 10.4 8.8 8.4 16.7 14.2 20.8 13.4 11.7 8.3 10.2 10.9 11 9.5 14.5 14.1 16.1 14.3 11.7 13.4 9.6 8.7 8.4 12.8 10.5 17.1 18.4 15.4 10.8 11.8 14.9 12.6 14.1 13 13.4 15.2 16.1 17.8 14.9 14.1 12.7 13.5 14.9 20 16.4 17.7 19.5 20.2 21.4 19.9 19 19.1 19.1 20.1 19.9 19.6 23.2 29.8 13.8 13.3 16.7 12 14.6 21.4 23 23.7 25 21.8 20.6 21.2 19.1 20.6 15.2 7 8.1 13.6 20.1 21.8 24.5 23.1 19.7 18.3 21.2 17.5 16.8 22.4 20.6 23.9 22 11.9
The data has 14 rows and 506 columns, where each column represents the 14 features of one house. The values in the last row represent the price of the property, and we will train a model to predict this value, given the remaining 13 features.
We also add a row of ones to the input matrix that will account for the bias (intercept) of our model and simplify the implementation.
1: 2: 3: 4: |
|
Our linear regression model is of the form
\[ h_{\mathbf{w}} (\mathbf{x}) = \sum_j w_j x_j = \mathbf{w}^{T} \mathbf{x}\]
which represents a family of linear functions parameterized by the vector \(\mathbf{w}\).
1:
|
|
For training the model, we minimize a loss function
\[ J(\mathbf{w}) = \frac{1}{2} \sum_{i=1}^{n} \left(h_{\mathbf{w}} (\mathbf{x}^{(i)}) - y^{(i)} \right)^2 = \frac{1}{2} \sum_{i=1}^{n} \left( \mathbf{w}^{T} \mathbf{x}^{(i)} - y^{(i)} \right)^2\]
where \(\mathbf{x}^{(i)}\) are vectors holding the 13 input features plus the bias input (the constant 1) and \(y^{(i)}\) are the target values (which are here scalar).
1: 2: 3: 4: 5: |
|
[12/11/2015 14:41:04] --- Training started [12/11/2015 14:41:04] Parameters : 14 [12/11/2015 14:41:04] Iterations : 1000 [12/11/2015 14:41:04] Epochs : 1000 [12/11/2015 14:41:04] Batches : Full (1 per epoch) [12/11/2015 14:41:04] Training data : 506 [12/11/2015 14:41:04] Validation data: None [12/11/2015 14:41:04] Valid. interval: 10 [12/11/2015 14:41:04] Method : Gradient descent [12/11/2015 14:41:04] Learning rate : RMSProp a0 = D 0.00100000005f, k = D 0.899999976f [12/11/2015 14:41:04] Momentum : None [12/11/2015 14:41:04] Loss : L2 norm [12/11/2015 14:41:04] Regularizer : L2 lambda = D 9.99999975e-05f [12/11/2015 14:41:04] Gradient clip. : None [12/11/2015 14:41:04] Early stopping : None [12/11/2015 14:41:04] Improv. thresh.: D 0.995000005f [12/11/2015 14:41:04] Return best : true [12/11/2015 14:41:04] 1/1000 | Batch 1/1 | D 5.281104e+002 [- ] [12/11/2015 14:41:04] 2/1000 | Batch 1/1 | D 5.252324e+002 [↓▼] [12/11/2015 14:41:04] 3/1000 | Batch 1/1 | D 5.231447e+002 [↓ ] [12/11/2015 14:41:04] 4/1000 | Batch 1/1 | D 5.213967e+002 [↓▼] [12/11/2015 14:41:04] 5/1000 | Batch 1/1 | D 5.198447e+002 [↓ ] [12/11/2015 14:41:04] 6/1000 | Batch 1/1 | D 5.184225e+002 [↓▼] [12/11/2015 14:41:04] 7/1000 | Batch 1/1 | D 5.170928e+002 [↓ ] ... [12/11/2015 14:41:27] 994/1000 | Batch 1/1 | D 6.404338e+000 [↓ ] [12/11/2015 14:41:27] 995/1000 | Batch 1/1 | D 6.392090e+000 [↓ ] [12/11/2015 14:41:27] 996/1000 | Batch 1/1 | D 6.377205e+000 [↓▼] [12/11/2015 14:41:28] 997/1000 | Batch 1/1 | D 6.363370e+000 [↓ ] [12/11/2015 14:41:28] 998/1000 | Batch 1/1 | D 6.351198e+000 [↓ ] [12/11/2015 14:41:28] 999/1000 | Batch 1/1 | D 6.344284e+000 [↓▼] [12/11/2015 14:41:28] 1000/1000 | Batch 1/1 | D 6.334455e+000 [↓ ] [12/11/2015 14:41:28] Duration : 00:00:23.3076639 [12/11/2015 14:41:28] Loss initial : D 5.281104e+002 [12/11/2015 14:41:28] Loss final : D 6.344284e+000 (Best) [12/11/2015 14:41:28] Loss change : D -5.217661e+002 (-98.80 %) [12/11/2015 14:41:28] Loss chg. / s : D -2.238603e+001 [12/11/2015 14:41:28] Epochs / s : 42.90434272 [12/11/2015 14:41:28] Epochs / min : 2574.260563 [12/11/2015 14:41:28] --- Training finishedval trainedmodel : (DV -> D)
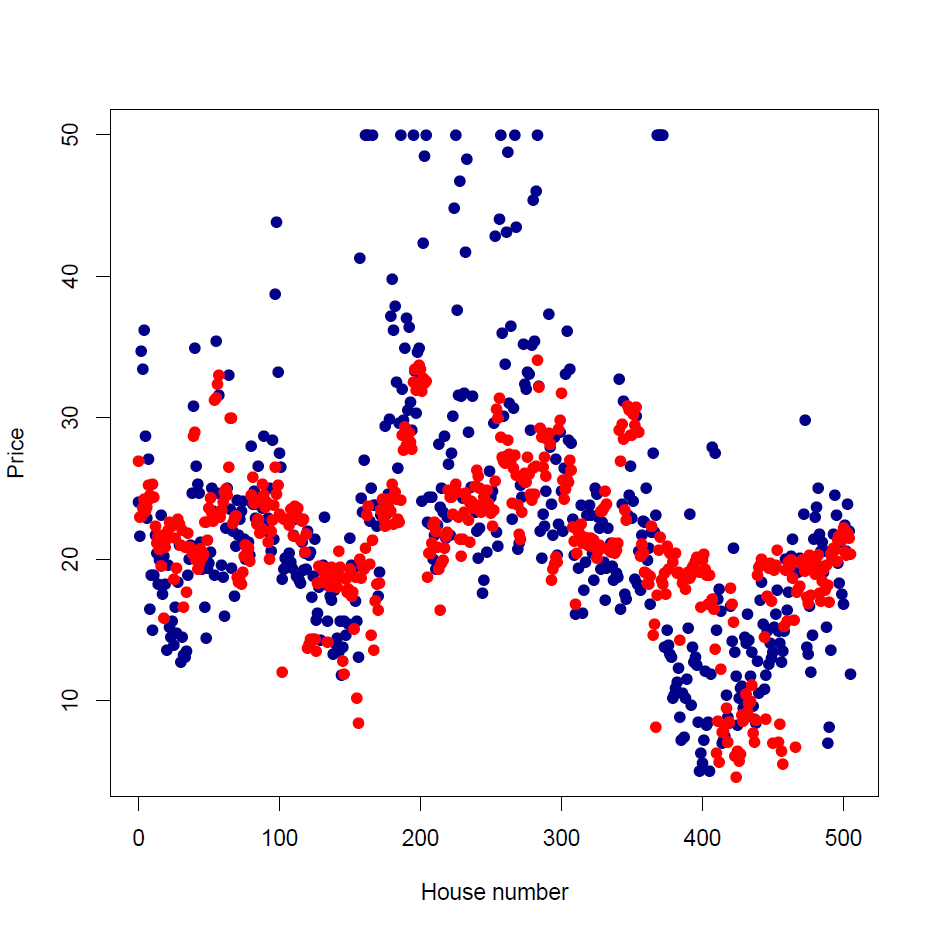
The following is a plot of the prices in the dataset where the blue points represent the real price, and the red points are the values predicted by the trained linear model.
Loss function
1: 2: 3: 4: 5: 6: |
|
Regularization
1: 2: 3: 4: 5: 6: |
|
Batch
1: 2: 3: 4: |
|
Validation and early stopping
1: 2: 3: 4: |
|
Training proceeds by minimizing the loss function by adjusting model parameters. Continuing this optimization for longer than necessary causes overfitting, where the model strives to precisely approximate the training data. Overfitting reduces the model's generalization ability and it's performance with new data in the field.
To prevent overfitting, data is divided into training and validation sets, and while the model is being optimized by computing the loss function using the training data, the model's performance with the validation data is also monitored. Generally, at the initial stages of training the loss for both the training and validation data will decrease. Eventually, the validation loss will asymptotically approach a minimum, and beyond a certain stage, it will start to increase even when the training loss keeps decreasing. This signifies a good time to stop the training, for preventing overfitting the model to the training data.
Hype does this via the EarlyStopping parameter, where you can specify a stagnation "patience" for the number of acceptable iterations for non-decreasing training loss and an overfitting patience for the number of acceptable iterations where the training loss decreases without an accompanying decrease in the validation loss.
Let's divide the housing dataset into training and validation sets and train the model using early stopping.
1: 2: |
|
val housingtrain : Dataset = Hype.Dataset X: 14 x 400 Y: 1 x 400 val housingvalid : Dataset = Hype.Dataset X: 14 x 106 Y: 1 x 106
1: 2: 3: 4: |
|
[12/11/2015 15:09:15] --- Training started [12/11/2015 15:09:15] Parameters : 14 [12/11/2015 15:09:15] Iterations : 1000 [12/11/2015 15:09:15] Epochs : 1000 [12/11/2015 15:09:15] Batches : Full (1 per epoch) [12/11/2015 15:09:15] Training data : 400 [12/11/2015 15:09:15] Validation data: 106 [12/11/2015 15:09:15] Valid. interval: 10 [12/11/2015 15:09:15] Method : Gradient descent [12/11/2015 15:09:15] Learning rate : RMSProp a0 = D 0.00100000005f, k = D 0.899999976f [12/11/2015 15:09:15] Momentum : None [12/11/2015 15:09:15] Loss : L2 norm [12/11/2015 15:09:15] Regularizer : L2 lambda = D 9.99999975e-05f [12/11/2015 15:09:15] Gradient clip. : None [12/11/2015 15:09:15] Early stopping : Stagnation thresh. = 750, overfit. thresh. = 10 [12/11/2015 15:09:15] Improv. thresh.: D 0.995000005f [12/11/2015 15:09:15] Return best : true [12/11/2015 15:09:15] 1/1000 | Batch 1/1 | D 3.221269e+002 [- ] | Valid D 3.322605e+002 [- ] | Stag: 0 Ovfit: 0 [12/11/2015 15:09:15] 2/1000 | Batch 1/1 | D 3.193867e+002 [↓▼] | Valid D 3.288632e+002 [↓▼] | Stag: 0 Ovfit: 0 [12/11/2015 15:09:15] 3/1000 | Batch 1/1 | D 3.173987e+002 [↓▼] | Valid D 3.263986e+002 [↓▼] | Stag: 0 Ovfit: 0 [12/11/2015 15:09:15] 4/1000 | Batch 1/1 | D 3.157341e+002 [↓▼] | Valid D 3.243348e+002 [↓▼] | Stag: 0 Ovfit: 0 [12/11/2015 15:09:15] 5/1000 | Batch 1/1 | D 3.142565e+002 [↓ ] | Valid D 3.225029e+002 [↓▼] | Stag: 0 Ovfit: 0 [12/11/2015 15:09:15] 6/1000 | Batch 1/1 | D 3.129025e+002 [↓▼] | Valid D 3.208241e+002 [↓▼] | Stag: 0 Ovfit: 0 [12/11/2015 15:09:15] 7/1000 | Batch 1/1 | D 3.116365e+002 [↓ ] | Valid D 3.192545e+002 [↓ ] | Stag: 10 Ovfit: 0 [12/11/2015 15:09:15] 8/1000 | Batch 1/1 | D 3.104370e+002 [↓▼] | Valid D 3.177671e+002 [↓▼] | Stag: 0 Ovfit: 0 [12/11/2015 15:09:15] 9/1000 | Batch 1/1 | D 3.092885e+002 [↓ ] | Valid D 3.163436e+002 [↓ ] | Stag: 10 Ovfit: 0 [12/11/2015 15:09:15] 10/1000 | Batch 1/1 | D 3.081814e+002 [↓▼] | Valid D 3.149709e+002 [↓▼] | Stag: 0 Ovfit: 0 [12/11/2015 15:09:15] 11/1000 | Batch 1/1 | D 3.071076e+002 [↓ ] | Valid D 3.136398e+002 [↓ ] | Stag: 10 Ovfit: 0 [12/11/2015 15:09:15] 12/1000 | Batch 1/1 | D 3.060618e+002 [↓▼] | Valid D 3.123428e+002 [↓▼] | Stag: 0 Ovfit: 0 [12/11/2015 15:09:15] 13/1000 | Batch 1/1 | D 3.050388e+002 [↓ ] | Valid D 3.110746e+002 [↓ ] | Stag: 10 Ovfit: 0 ... [12/11/2015 15:09:21] 318/1000 | Batch 1/1 | D 4.250416e+001 [↓▼] | Valid D 3.382476e+001 [↓▼] | Stag: 0 Ovfit: 0 [12/11/2015 15:09:21] 319/1000 | Batch 1/1 | D 4.178834e+001 [↓▼] | Valid D 3.371201e+001 [↓ ] | Stag: 10 Ovfit: 0 [12/11/2015 15:09:21] 320/1000 | Batch 1/1 | D 4.109373e+001 [↓▼] | Valid D 3.361367e+001 [↓▼] | Stag: 0 Ovfit: 0 [12/11/2015 15:09:21] 321/1000 | Batch 1/1 | D 4.040976e+001 [↓▼] | Valid D 3.362166e+001 [↑ ] | Stag: 10 Ovfit: 0 [12/11/2015 15:09:21] 322/1000 | Batch 1/1 | D 3.973472e+001 [↓▼] | Valid D 3.368684e+001 [↑ ] | Stag: 20 Ovfit: 1 [12/11/2015 15:09:21] 323/1000 | Batch 1/1 | D 3.907929e+001 [↓▼] | Valid D 3.382304e+001 [↑ ] | Stag: 30 Ovfit: 2 [12/11/2015 15:09:21] 324/1000 | Batch 1/1 | D 3.845267e+001 [↓▼] | Valid D 3.398524e+001 [↑ ] | Stag: 40 Ovfit: 3 [12/11/2015 15:09:21] 325/1000 | Batch 1/1 | D 3.783842e+001 [↓▼] | Valid D 3.418199e+001 [↑ ] | Stag: 50 Ovfit: 4 [12/11/2015 15:09:21] 326/1000 | Batch 1/1 | D 3.721857e+001 [↓▼] | Valid D 3.450164e+001 [↑ ] | Stag: 60 Ovfit: 5 [12/11/2015 15:09:21] 327/1000 | Batch 1/1 | D 3.659464e+001 [↓▼] | Valid D 3.499456e+001 [↑ ] | Stag: 70 Ovfit: 6 [12/11/2015 15:09:21] 328/1000 | Batch 1/1 | D 3.598552e+001 [↓▼] | Valid D 3.556280e+001 [↑ ] | Stag: 80 Ovfit: 7 [12/11/2015 15:09:21] 329/1000 | Batch 1/1 | D 3.538885e+001 [↓▼] | Valid D 3.616002e+001 [↑ ] | Stag: 90 Ovfit: 8 [12/11/2015 15:09:21] 330/1000 | Batch 1/1 | D 3.481464e+001 [↓▼] | Valid D 3.678414e+001 [↑ ] | Stag:100 Ovfit: 9 [12/11/2015 15:09:21] *** EARLY STOPPING TRIGGERED: Overfitting *** [12/11/2015 15:09:21] 331/1000 | Batch 1/1 | D 3.426452e+001 [↓▼] | Valid D 3.741238e+001 [↑ ] | Stag:110 Ovfit:10 [12/11/2015 15:09:21] Duration : 00:00:05.9617220 [12/11/2015 15:09:21] Loss initial : D 3.221269e+002 [12/11/2015 15:09:21] Loss final : D 3.373809e+001 (Best) [12/11/2015 15:09:21] Loss change : D -2.883888e+002 (-89.53 %) [12/11/2015 15:09:21] Loss chg. / s : D -4.837340e+001 [12/11/2015 15:09:21] Epochs / s : 55.52087132 [12/11/2015 15:09:21] Epochs / min : 3331.252279 [12/11/2015 15:09:21] --- Training finished
namespace System
type Environment =
static member CommandLine : string
static member CurrentDirectory : string with get, set
static member Exit : exitCode:int -> unit
static member ExitCode : int with get, set
static member ExpandEnvironmentVariables : name:string -> string
static member FailFast : message:string -> unit + 1 overload
static member GetCommandLineArgs : unit -> string[]
static member GetEnvironmentVariable : variable:string -> string + 1 overload
static member GetEnvironmentVariables : unit -> IDictionary + 1 overload
static member GetFolderPath : folder:SpecialFolder -> string + 1 overload
...
nested type SpecialFolder
nested type SpecialFolderOption
Full name: System.Environment
static member CommandLine : string
static member CurrentDirectory : string with get, set
static member Exit : exitCode:int -> unit
static member ExitCode : int with get, set
static member ExpandEnvironmentVariables : name:string -> string
static member FailFast : message:string -> unit + 1 overload
static member GetCommandLineArgs : unit -> string[]
static member GetEnvironmentVariable : variable:string -> string + 1 overload
static member GetEnvironmentVariables : unit -> IDictionary + 1 overload
static member GetFolderPath : folder:SpecialFolder -> string + 1 overload
...
nested type SpecialFolder
nested type SpecialFolderOption
Full name: System.Environment
property System.Environment.CurrentDirectory: string
namespace Hype
namespace DiffSharp
namespace DiffSharp.AD
module Float32
from DiffSharp.AD
from DiffSharp.AD
val x : DM
Full name: Training.x
Full name: Training.x
val toDM : m:seq<seq<'a>> -> DM (requires member op_Explicit)
Full name: DiffSharp.AD.Float32.DOps.toDM
Full name: DiffSharp.AD.Float32.DOps.toDM
val y : DM
Full name: Training.y
Full name: Training.y
val XORdata : Dataset
Full name: Training.XORdata
Full name: Training.XORdata
Multiple items
type Dataset =
new : s:seq<DV * DV> -> Dataset
new : xi:seq<int> * y:DM -> Dataset
new : x:DM * yi:seq<int> -> Dataset
new : xi:seq<int> * yi:seq<int> -> Dataset
new : x:DM * y:DM -> Dataset
new : xi:seq<int> * onehotdimsx:int * y:DM -> Dataset
new : x:DM * yi:seq<int> * onehotdimsy:int -> Dataset
new : xi:seq<int> * onehotdimsx:int * yi:seq<int> * onehotdimsy:int -> Dataset
private new : x:DM * y:DM * xi:seq<int> * yi:seq<int> -> Dataset
member AppendBiasRowX : unit -> Dataset
...
Full name: Hype.Dataset
--------------------
new : s:seq<DV * DV> -> Dataset
new : x:DM * y:DM -> Dataset
new : xi:seq<int> * yi:seq<int> -> Dataset
new : x:DM * yi:seq<int> -> Dataset
new : xi:seq<int> * y:DM -> Dataset
new : x:DM * yi:seq<int> * onehotdimsy:int -> Dataset
new : xi:seq<int> * onehotdimsx:int * y:DM -> Dataset
new : xi:seq<int> * onehotdimsx:int * yi:seq<int> * onehotdimsy:int -> Dataset
type Dataset =
new : s:seq<DV * DV> -> Dataset
new : xi:seq<int> * y:DM -> Dataset
new : x:DM * yi:seq<int> -> Dataset
new : xi:seq<int> * yi:seq<int> -> Dataset
new : x:DM * y:DM -> Dataset
new : xi:seq<int> * onehotdimsx:int * y:DM -> Dataset
new : x:DM * yi:seq<int> * onehotdimsy:int -> Dataset
new : xi:seq<int> * onehotdimsx:int * yi:seq<int> * onehotdimsy:int -> Dataset
private new : x:DM * y:DM * xi:seq<int> * yi:seq<int> -> Dataset
member AppendBiasRowX : unit -> Dataset
...
Full name: Hype.Dataset
--------------------
new : s:seq<DV * DV> -> Dataset
new : x:DM * y:DM -> Dataset
new : xi:seq<int> * yi:seq<int> -> Dataset
new : x:DM * yi:seq<int> -> Dataset
new : xi:seq<int> * y:DM -> Dataset
new : x:DM * yi:seq<int> * onehotdimsy:int -> Dataset
new : xi:seq<int> * onehotdimsx:int * y:DM -> Dataset
new : xi:seq<int> * onehotdimsx:int * yi:seq<int> * onehotdimsy:int -> Dataset
val MNIST : Dataset
Full name: Training.MNIST
Full name: Training.MNIST
type Util =
static member LoadDelimited : filename:string -> DM
static member LoadDelimited : filename:string * separators:char [] -> DM
static member LoadImage : filename:string -> DM
static member LoadMNISTLabels : filename:string -> int []
static member LoadMNISTLabels : filename:string * n:int -> int []
static member LoadMNISTPixels : filename:string -> DM
static member LoadMNISTPixels : filename:string * n:int -> DM
static member VisualizeDMRowsAsImageGrid : w:DM * imagerows:int -> string
static member printLog : s:string -> unit
static member printModel : f:(DV -> DV) -> d:Dataset -> unit
Full name: Hype.Util
static member LoadDelimited : filename:string -> DM
static member LoadDelimited : filename:string * separators:char [] -> DM
static member LoadImage : filename:string -> DM
static member LoadMNISTLabels : filename:string -> int []
static member LoadMNISTLabels : filename:string * n:int -> int []
static member LoadMNISTPixels : filename:string -> DM
static member LoadMNISTPixels : filename:string * n:int -> DM
static member VisualizeDMRowsAsImageGrid : w:DM * imagerows:int -> string
static member printLog : s:string -> unit
static member printModel : f:(DV -> DV) -> d:Dataset -> unit
Full name: Hype.Util
static member Util.LoadMNISTPixels : filename:string -> DM
static member Util.LoadMNISTPixels : filename:string * n:int -> DM
static member Util.LoadMNISTPixels : filename:string * n:int -> DM
static member Util.LoadMNISTLabels : filename:string -> int []
static member Util.LoadMNISTLabels : filename:string * n:int -> int []
static member Util.LoadMNISTLabels : filename:string * n:int -> int []
val toDV : v:seq<'a> -> DV (requires member op_Explicit)
Full name: DiffSharp.AD.Float32.DOps.toDV
Full name: DiffSharp.AD.Float32.DOps.toDV
Multiple items
union case DM.DM: float32 [,] -> DM
--------------------
module DM
from DiffSharp.AD.Float32
--------------------
type DM =
| DM of float32 [,]
| DMF of DM * DM * uint32
| DMR of DM * DM ref * TraceOp * uint32 ref * uint32
member Copy : unit -> DM
member GetCols : unit -> seq<DV>
member GetForward : t:DM * i:uint32 -> DM
member GetReverse : i:uint32 -> DM
member GetRows : unit -> seq<DV>
member GetSlice : rowStart:int option * rowFinish:int option * col:int -> DV
member GetSlice : row:int * colStart:int option * colFinish:int option -> DV
member GetSlice : rowStart:int option * rowFinish:int option * colStart:int option * colFinish:int option -> DM
member ToMathematicaString : unit -> string
member ToMatlabString : unit -> string
override ToString : unit -> string
member Visualize : unit -> string
member A : DM
member Cols : int
member F : uint32
member Item : i:int * j:int -> D with get
member Length : int
member P : DM
member PD : DM
member Rows : int
member T : DM
member A : DM with set
member F : uint32 with set
static member Abs : a:DM -> DM
static member Acos : a:DM -> DM
static member AddDiagonal : a:DM * b:DV -> DM
static member AddItem : a:DM * i:int * j:int * b:D -> DM
static member AddSubMatrix : a:DM * i:int * j:int * b:DM -> DM
static member Asin : a:DM -> DM
static member Atan : a:DM -> DM
static member Atan2 : a:int * b:DM -> DM
static member Atan2 : a:DM * b:int -> DM
static member Atan2 : a:float32 * b:DM -> DM
static member Atan2 : a:DM * b:float32 -> DM
static member Atan2 : a:D * b:DM -> DM
static member Atan2 : a:DM * b:D -> DM
static member Atan2 : a:DM * b:DM -> DM
static member Ceiling : a:DM -> DM
static member Cos : a:DM -> DM
static member Cosh : a:DM -> DM
static member Det : a:DM -> D
static member Diagonal : a:DM -> DV
static member Exp : a:DM -> DM
static member Floor : a:DM -> DM
static member Inverse : a:DM -> DM
static member Log : a:DM -> DM
static member Log10 : a:DM -> DM
static member Max : a:DM -> D
static member Max : a:D * b:DM -> DM
static member Max : a:DM * b:D -> DM
static member Max : a:DM * b:DM -> DM
static member MaxIndex : a:DM -> int * int
static member Mean : a:DM -> D
static member Min : a:DM -> D
static member Min : a:D * b:DM -> DM
static member Min : a:DM * b:D -> DM
static member Min : a:DM * b:DM -> DM
static member MinIndex : a:DM -> int * int
static member Normalize : a:DM -> DM
static member OfArray : m:int * a:D [] -> DM
static member OfArray2D : a:D [,] -> DM
static member OfCols : n:int * a:DV -> DM
static member OfRows : s:seq<DV> -> DM
static member OfRows : m:int * a:DV -> DM
static member Op_DM_D : a:DM * ff:(float32 [,] -> float32) * fd:(DM -> D) * df:(D * DM * DM -> D) * r:(DM -> TraceOp) -> D
static member Op_DM_DM : a:DM * ff:(float32 [,] -> float32 [,]) * fd:(DM -> DM) * df:(DM * DM * DM -> DM) * r:(DM -> TraceOp) -> DM
static member Op_DM_DM_DM : a:DM * b:DM * ff:(float32 [,] * float32 [,] -> float32 [,]) * fd:(DM * DM -> DM) * df_da:(DM * DM * DM -> DM) * df_db:(DM * DM * DM -> DM) * df_dab:(DM * DM * DM * DM * DM -> DM) * r_d_d:(DM * DM -> TraceOp) * r_d_c:(DM * DM -> TraceOp) * r_c_d:(DM * DM -> TraceOp) -> DM
static member Op_DM_DV : a:DM * ff:(float32 [,] -> float32 []) * fd:(DM -> DV) * df:(DV * DM * DM -> DV) * r:(DM -> TraceOp) -> DV
static member Op_DM_DV_DM : a:DM * b:DV * ff:(float32 [,] * float32 [] -> float32 [,]) * fd:(DM * DV -> DM) * df_da:(DM * DM * DM -> DM) * df_db:(DM * DV * DV -> DM) * df_dab:(DM * DM * DM * DV * DV -> DM) * r_d_d:(DM * DV -> TraceOp) * r_d_c:(DM * DV -> TraceOp) * r_c_d:(DM * DV -> TraceOp) -> DM
static member Op_DM_DV_DV : a:DM * b:DV * ff:(float32 [,] * float32 [] -> float32 []) * fd:(DM * DV -> DV) * df_da:(DV * DM * DM -> DV) * df_db:(DV * DV * DV -> DV) * df_dab:(DV * DM * DM * DV * DV -> DV) * r_d_d:(DM * DV -> TraceOp) * r_d_c:(DM * DV -> TraceOp) * r_c_d:(DM * DV -> TraceOp) -> DV
static member Op_DM_D_DM : a:DM * b:D * ff:(float32 [,] * float32 -> float32 [,]) * fd:(DM * D -> DM) * df_da:(DM * DM * DM -> DM) * df_db:(DM * D * D -> DM) * df_dab:(DM * DM * DM * D * D -> DM) * r_d_d:(DM * D -> TraceOp) * r_d_c:(DM * D -> TraceOp) * r_c_d:(DM * D -> TraceOp) -> DM
static member Op_DV_DM_DM : a:DV * b:DM * ff:(float32 [] * float32 [,] -> float32 [,]) * fd:(DV * DM -> DM) * df_da:(DM * DV * DV -> DM) * df_db:(DM * DM * DM -> DM) * df_dab:(DM * DV * DV * DM * DM -> DM) * r_d_d:(DV * DM -> TraceOp) * r_d_c:(DV * DM -> TraceOp) * r_c_d:(DV * DM -> TraceOp) -> DM
static member Op_DV_DM_DV : a:DV * b:DM * ff:(float32 [] * float32 [,] -> float32 []) * fd:(DV * DM -> DV) * df_da:(DV * DV * DV -> DV) * df_db:(DV * DM * DM -> DV) * df_dab:(DV * DV * DV * DM * DM -> DV) * r_d_d:(DV * DM -> TraceOp) * r_d_c:(DV * DM -> TraceOp) * r_c_d:(DV * DM -> TraceOp) -> DV
static member Op_D_DM_DM : a:D * b:DM * ff:(float32 * float32 [,] -> float32 [,]) * fd:(D * DM -> DM) * df_da:(DM * D * D -> DM) * df_db:(DM * DM * DM -> DM) * df_dab:(DM * D * D * DM * DM -> DM) * r_d_d:(D * DM -> TraceOp) * r_d_c:(D * DM -> TraceOp) * r_c_d:(D * DM -> TraceOp) -> DM
static member Pow : a:int * b:DM -> DM
static member Pow : a:DM * b:int -> DM
static member Pow : a:float32 * b:DM -> DM
static member Pow : a:DM * b:float32 -> DM
static member Pow : a:D * b:DM -> DM
static member Pow : a:DM * b:D -> DM
static member Pow : a:DM * b:DM -> DM
static member ReLU : a:DM -> DM
static member ReshapeToDV : a:DM -> DV
static member Round : a:DM -> DM
static member Sigmoid : a:DM -> DM
static member Sign : a:DM -> DM
static member Sin : a:DM -> DM
static member Sinh : a:DM -> DM
static member SoftPlus : a:DM -> DM
static member SoftSign : a:DM -> DM
static member Solve : a:DM * b:DV -> DV
static member SolveSymmetric : a:DM * b:DV -> DV
static member Sqrt : a:DM -> DM
static member StandardDev : a:DM -> D
static member Standardize : a:DM -> DM
static member Sum : a:DM -> D
static member Tan : a:DM -> DM
static member Tanh : a:DM -> DM
static member Trace : a:DM -> D
static member Transpose : a:DM -> DM
static member Variance : a:DM -> D
static member ZeroMN : m:int -> n:int -> DM
static member Zero : DM
static member ( + ) : a:int * b:DM -> DM
static member ( + ) : a:DM * b:int -> DM
static member ( + ) : a:float32 * b:DM -> DM
static member ( + ) : a:DM * b:float32 -> DM
static member ( + ) : a:DM * b:DV -> DM
static member ( + ) : a:DV * b:DM -> DM
static member ( + ) : a:D * b:DM -> DM
static member ( + ) : a:DM * b:D -> DM
static member ( + ) : a:DM * b:DM -> DM
static member ( / ) : a:int * b:DM -> DM
static member ( / ) : a:DM * b:int -> DM
static member ( / ) : a:float32 * b:DM -> DM
static member ( / ) : a:DM * b:float32 -> DM
static member ( / ) : a:D * b:DM -> DM
static member ( / ) : a:DM * b:D -> DM
static member ( ./ ) : a:DM * b:DM -> DM
static member ( .* ) : a:DM * b:DM -> DM
static member op_Explicit : d:float32 [,] -> DM
static member op_Explicit : d:DM -> float32 [,]
static member ( * ) : a:int * b:DM -> DM
static member ( * ) : a:DM * b:int -> DM
static member ( * ) : a:float32 * b:DM -> DM
static member ( * ) : a:DM * b:float32 -> DM
static member ( * ) : a:D * b:DM -> DM
static member ( * ) : a:DM * b:D -> DM
static member ( * ) : a:DV * b:DM -> DV
static member ( * ) : a:DM * b:DV -> DV
static member ( * ) : a:DM * b:DM -> DM
static member ( - ) : a:int * b:DM -> DM
static member ( - ) : a:DM * b:int -> DM
static member ( - ) : a:float32 * b:DM -> DM
static member ( - ) : a:DM * b:float32 -> DM
static member ( - ) : a:D * b:DM -> DM
static member ( - ) : a:DM * b:D -> DM
static member ( - ) : a:DM * b:DM -> DM
static member ( ~- ) : a:DM -> DM
Full name: DiffSharp.AD.Float32.DM
union case DM.DM: float32 [,] -> DM
--------------------
module DM
from DiffSharp.AD.Float32
--------------------
type DM =
| DM of float32 [,]
| DMF of DM * DM * uint32
| DMR of DM * DM ref * TraceOp * uint32 ref * uint32
member Copy : unit -> DM
member GetCols : unit -> seq<DV>
member GetForward : t:DM * i:uint32 -> DM
member GetReverse : i:uint32 -> DM
member GetRows : unit -> seq<DV>
member GetSlice : rowStart:int option * rowFinish:int option * col:int -> DV
member GetSlice : row:int * colStart:int option * colFinish:int option -> DV
member GetSlice : rowStart:int option * rowFinish:int option * colStart:int option * colFinish:int option -> DM
member ToMathematicaString : unit -> string
member ToMatlabString : unit -> string
override ToString : unit -> string
member Visualize : unit -> string
member A : DM
member Cols : int
member F : uint32
member Item : i:int * j:int -> D with get
member Length : int
member P : DM
member PD : DM
member Rows : int
member T : DM
member A : DM with set
member F : uint32 with set
static member Abs : a:DM -> DM
static member Acos : a:DM -> DM
static member AddDiagonal : a:DM * b:DV -> DM
static member AddItem : a:DM * i:int * j:int * b:D -> DM
static member AddSubMatrix : a:DM * i:int * j:int * b:DM -> DM
static member Asin : a:DM -> DM
static member Atan : a:DM -> DM
static member Atan2 : a:int * b:DM -> DM
static member Atan2 : a:DM * b:int -> DM
static member Atan2 : a:float32 * b:DM -> DM
static member Atan2 : a:DM * b:float32 -> DM
static member Atan2 : a:D * b:DM -> DM
static member Atan2 : a:DM * b:D -> DM
static member Atan2 : a:DM * b:DM -> DM
static member Ceiling : a:DM -> DM
static member Cos : a:DM -> DM
static member Cosh : a:DM -> DM
static member Det : a:DM -> D
static member Diagonal : a:DM -> DV
static member Exp : a:DM -> DM
static member Floor : a:DM -> DM
static member Inverse : a:DM -> DM
static member Log : a:DM -> DM
static member Log10 : a:DM -> DM
static member Max : a:DM -> D
static member Max : a:D * b:DM -> DM
static member Max : a:DM * b:D -> DM
static member Max : a:DM * b:DM -> DM
static member MaxIndex : a:DM -> int * int
static member Mean : a:DM -> D
static member Min : a:DM -> D
static member Min : a:D * b:DM -> DM
static member Min : a:DM * b:D -> DM
static member Min : a:DM * b:DM -> DM
static member MinIndex : a:DM -> int * int
static member Normalize : a:DM -> DM
static member OfArray : m:int * a:D [] -> DM
static member OfArray2D : a:D [,] -> DM
static member OfCols : n:int * a:DV -> DM
static member OfRows : s:seq<DV> -> DM
static member OfRows : m:int * a:DV -> DM
static member Op_DM_D : a:DM * ff:(float32 [,] -> float32) * fd:(DM -> D) * df:(D * DM * DM -> D) * r:(DM -> TraceOp) -> D
static member Op_DM_DM : a:DM * ff:(float32 [,] -> float32 [,]) * fd:(DM -> DM) * df:(DM * DM * DM -> DM) * r:(DM -> TraceOp) -> DM
static member Op_DM_DM_DM : a:DM * b:DM * ff:(float32 [,] * float32 [,] -> float32 [,]) * fd:(DM * DM -> DM) * df_da:(DM * DM * DM -> DM) * df_db:(DM * DM * DM -> DM) * df_dab:(DM * DM * DM * DM * DM -> DM) * r_d_d:(DM * DM -> TraceOp) * r_d_c:(DM * DM -> TraceOp) * r_c_d:(DM * DM -> TraceOp) -> DM
static member Op_DM_DV : a:DM * ff:(float32 [,] -> float32 []) * fd:(DM -> DV) * df:(DV * DM * DM -> DV) * r:(DM -> TraceOp) -> DV
static member Op_DM_DV_DM : a:DM * b:DV * ff:(float32 [,] * float32 [] -> float32 [,]) * fd:(DM * DV -> DM) * df_da:(DM * DM * DM -> DM) * df_db:(DM * DV * DV -> DM) * df_dab:(DM * DM * DM * DV * DV -> DM) * r_d_d:(DM * DV -> TraceOp) * r_d_c:(DM * DV -> TraceOp) * r_c_d:(DM * DV -> TraceOp) -> DM
static member Op_DM_DV_DV : a:DM * b:DV * ff:(float32 [,] * float32 [] -> float32 []) * fd:(DM * DV -> DV) * df_da:(DV * DM * DM -> DV) * df_db:(DV * DV * DV -> DV) * df_dab:(DV * DM * DM * DV * DV -> DV) * r_d_d:(DM * DV -> TraceOp) * r_d_c:(DM * DV -> TraceOp) * r_c_d:(DM * DV -> TraceOp) -> DV
static member Op_DM_D_DM : a:DM * b:D * ff:(float32 [,] * float32 -> float32 [,]) * fd:(DM * D -> DM) * df_da:(DM * DM * DM -> DM) * df_db:(DM * D * D -> DM) * df_dab:(DM * DM * DM * D * D -> DM) * r_d_d:(DM * D -> TraceOp) * r_d_c:(DM * D -> TraceOp) * r_c_d:(DM * D -> TraceOp) -> DM
static member Op_DV_DM_DM : a:DV * b:DM * ff:(float32 [] * float32 [,] -> float32 [,]) * fd:(DV * DM -> DM) * df_da:(DM * DV * DV -> DM) * df_db:(DM * DM * DM -> DM) * df_dab:(DM * DV * DV * DM * DM -> DM) * r_d_d:(DV * DM -> TraceOp) * r_d_c:(DV * DM -> TraceOp) * r_c_d:(DV * DM -> TraceOp) -> DM
static member Op_DV_DM_DV : a:DV * b:DM * ff:(float32 [] * float32 [,] -> float32 []) * fd:(DV * DM -> DV) * df_da:(DV * DV * DV -> DV) * df_db:(DV * DM * DM -> DV) * df_dab:(DV * DV * DV * DM * DM -> DV) * r_d_d:(DV * DM -> TraceOp) * r_d_c:(DV * DM -> TraceOp) * r_c_d:(DV * DM -> TraceOp) -> DV
static member Op_D_DM_DM : a:D * b:DM * ff:(float32 * float32 [,] -> float32 [,]) * fd:(D * DM -> DM) * df_da:(DM * D * D -> DM) * df_db:(DM * DM * DM -> DM) * df_dab:(DM * D * D * DM * DM -> DM) * r_d_d:(D * DM -> TraceOp) * r_d_c:(D * DM -> TraceOp) * r_c_d:(D * DM -> TraceOp) -> DM
static member Pow : a:int * b:DM -> DM
static member Pow : a:DM * b:int -> DM
static member Pow : a:float32 * b:DM -> DM
static member Pow : a:DM * b:float32 -> DM
static member Pow : a:D * b:DM -> DM
static member Pow : a:DM * b:D -> DM
static member Pow : a:DM * b:DM -> DM
static member ReLU : a:DM -> DM
static member ReshapeToDV : a:DM -> DV
static member Round : a:DM -> DM
static member Sigmoid : a:DM -> DM
static member Sign : a:DM -> DM
static member Sin : a:DM -> DM
static member Sinh : a:DM -> DM
static member SoftPlus : a:DM -> DM
static member SoftSign : a:DM -> DM
static member Solve : a:DM * b:DV -> DV
static member SolveSymmetric : a:DM * b:DV -> DV
static member Sqrt : a:DM -> DM
static member StandardDev : a:DM -> D
static member Standardize : a:DM -> DM
static member Sum : a:DM -> D
static member Tan : a:DM -> DM
static member Tanh : a:DM -> DM
static member Trace : a:DM -> D
static member Transpose : a:DM -> DM
static member Variance : a:DM -> D
static member ZeroMN : m:int -> n:int -> DM
static member Zero : DM
static member ( + ) : a:int * b:DM -> DM
static member ( + ) : a:DM * b:int -> DM
static member ( + ) : a:float32 * b:DM -> DM
static member ( + ) : a:DM * b:float32 -> DM
static member ( + ) : a:DM * b:DV -> DM
static member ( + ) : a:DV * b:DM -> DM
static member ( + ) : a:D * b:DM -> DM
static member ( + ) : a:DM * b:D -> DM
static member ( + ) : a:DM * b:DM -> DM
static member ( / ) : a:int * b:DM -> DM
static member ( / ) : a:DM * b:int -> DM
static member ( / ) : a:float32 * b:DM -> DM
static member ( / ) : a:DM * b:float32 -> DM
static member ( / ) : a:D * b:DM -> DM
static member ( / ) : a:DM * b:D -> DM
static member ( ./ ) : a:DM * b:DM -> DM
static member ( .* ) : a:DM * b:DM -> DM
static member op_Explicit : d:float32 [,] -> DM
static member op_Explicit : d:DM -> float32 [,]
static member ( * ) : a:int * b:DM -> DM
static member ( * ) : a:DM * b:int -> DM
static member ( * ) : a:float32 * b:DM -> DM
static member ( * ) : a:DM * b:float32 -> DM
static member ( * ) : a:D * b:DM -> DM
static member ( * ) : a:DM * b:D -> DM
static member ( * ) : a:DV * b:DM -> DV
static member ( * ) : a:DM * b:DV -> DV
static member ( * ) : a:DM * b:DM -> DM
static member ( - ) : a:int * b:DM -> DM
static member ( - ) : a:DM * b:int -> DM
static member ( - ) : a:float32 * b:DM -> DM
static member ( - ) : a:DM * b:float32 -> DM
static member ( - ) : a:D * b:DM -> DM
static member ( - ) : a:DM * b:D -> DM
static member ( - ) : a:DM * b:DM -> DM
static member ( ~- ) : a:DM -> DM
Full name: DiffSharp.AD.Float32.DM
val ofDV : m:int -> v:DV -> DM
Full name: DiffSharp.AD.Float32.DM.ofDV
Full name: DiffSharp.AD.Float32.DM.ofDV
val MNISTtest : Dataset
Full name: Training.MNISTtest
Full name: Training.MNISTtest
val h : DM
Full name: Training.h
Full name: Training.h
static member Util.LoadDelimited : filename:string -> DM
static member Util.LoadDelimited : filename:string * separators:char [] -> DM
static member Util.LoadDelimited : filename:string * separators:char [] -> DM
static member DM.Transpose : a:DM -> DM
override DM.ToString : unit -> string
val printfn : format:Printf.TextWriterFormat<'T> -> 'T
Full name: Microsoft.FSharp.Core.ExtraTopLevelOperators.printfn
Full name: Microsoft.FSharp.Core.ExtraTopLevelOperators.printfn
val hx : DM
Full name: Training.hx
Full name: Training.hx
val hy : DM
Full name: Training.hy
Full name: Training.hy
val housing : Dataset
Full name: Training.housing
Full name: Training.housing
val model : w:DV -> x:DV -> D
Full name: Training.model
Full name: Training.model
val w : DV
Multiple items
union case DV.DV: float32 [] -> DV
--------------------
module DV
from DiffSharp.AD.Float32
--------------------
type DV =
| DV of float32 []
| DVF of DV * DV * uint32
| DVR of DV * DV ref * TraceOp * uint32 ref * uint32
member Copy : unit -> DV
member GetForward : t:DV * i:uint32 -> DV
member GetReverse : i:uint32 -> DV
member GetSlice : lower:int option * upper:int option -> DV
member ToArray : unit -> D []
member ToColDM : unit -> DM
member ToMathematicaString : unit -> string
member ToMatlabString : unit -> string
member ToRowDM : unit -> DM
override ToString : unit -> string
member Visualize : unit -> string
member A : DV
member F : uint32
member Item : i:int -> D with get
member Length : int
member P : DV
member PD : DV
member T : DV
member A : DV with set
member F : uint32 with set
static member Abs : a:DV -> DV
static member Acos : a:DV -> DV
static member AddItem : a:DV * i:int * b:D -> DV
static member AddSubVector : a:DV * i:int * b:DV -> DV
static member Append : a:DV * b:DV -> DV
static member Asin : a:DV -> DV
static member Atan : a:DV -> DV
static member Atan2 : a:int * b:DV -> DV
static member Atan2 : a:DV * b:int -> DV
static member Atan2 : a:float32 * b:DV -> DV
static member Atan2 : a:DV * b:float32 -> DV
static member Atan2 : a:D * b:DV -> DV
static member Atan2 : a:DV * b:D -> DV
static member Atan2 : a:DV * b:DV -> DV
static member Ceiling : a:DV -> DV
static member Cos : a:DV -> DV
static member Cosh : a:DV -> DV
static member Exp : a:DV -> DV
static member Floor : a:DV -> DV
static member L1Norm : a:DV -> D
static member L2Norm : a:DV -> D
static member L2NormSq : a:DV -> D
static member Log : a:DV -> DV
static member Log10 : a:DV -> DV
static member LogSumExp : a:DV -> D
static member Max : a:DV -> D
static member Max : a:D * b:DV -> DV
static member Max : a:DV * b:D -> DV
static member Max : a:DV * b:DV -> DV
static member MaxIndex : a:DV -> int
static member Mean : a:DV -> D
static member Min : a:DV -> D
static member Min : a:D * b:DV -> DV
static member Min : a:DV * b:D -> DV
static member Min : a:DV * b:DV -> DV
static member MinIndex : a:DV -> int
static member Normalize : a:DV -> DV
static member OfArray : a:D [] -> DV
static member Op_DV_D : a:DV * ff:(float32 [] -> float32) * fd:(DV -> D) * df:(D * DV * DV -> D) * r:(DV -> TraceOp) -> D
static member Op_DV_DM : a:DV * ff:(float32 [] -> float32 [,]) * fd:(DV -> DM) * df:(DM * DV * DV -> DM) * r:(DV -> TraceOp) -> DM
static member Op_DV_DV : a:DV * ff:(float32 [] -> float32 []) * fd:(DV -> DV) * df:(DV * DV * DV -> DV) * r:(DV -> TraceOp) -> DV
static member Op_DV_DV_D : a:DV * b:DV * ff:(float32 [] * float32 [] -> float32) * fd:(DV * DV -> D) * df_da:(D * DV * DV -> D) * df_db:(D * DV * DV -> D) * df_dab:(D * DV * DV * DV * DV -> D) * r_d_d:(DV * DV -> TraceOp) * r_d_c:(DV * DV -> TraceOp) * r_c_d:(DV * DV -> TraceOp) -> D
static member Op_DV_DV_DM : a:DV * b:DV * ff:(float32 [] * float32 [] -> float32 [,]) * fd:(DV * DV -> DM) * df_da:(DM * DV * DV -> DM) * df_db:(DM * DV * DV -> DM) * df_dab:(DM * DV * DV * DV * DV -> DM) * r_d_d:(DV * DV -> TraceOp) * r_d_c:(DV * DV -> TraceOp) * r_c_d:(DV * DV -> TraceOp) -> DM
static member Op_DV_DV_DV : a:DV * b:DV * ff:(float32 [] * float32 [] -> float32 []) * fd:(DV * DV -> DV) * df_da:(DV * DV * DV -> DV) * df_db:(DV * DV * DV -> DV) * df_dab:(DV * DV * DV * DV * DV -> DV) * r_d_d:(DV * DV -> TraceOp) * r_d_c:(DV * DV -> TraceOp) * r_c_d:(DV * DV -> TraceOp) -> DV
static member Op_DV_D_DV : a:DV * b:D * ff:(float32 [] * float32 -> float32 []) * fd:(DV * D -> DV) * df_da:(DV * DV * DV -> DV) * df_db:(DV * D * D -> DV) * df_dab:(DV * DV * DV * D * D -> DV) * r_d_d:(DV * D -> TraceOp) * r_d_c:(DV * D -> TraceOp) * r_c_d:(DV * D -> TraceOp) -> DV
static member Op_D_DV_DV : a:D * b:DV * ff:(float32 * float32 [] -> float32 []) * fd:(D * DV -> DV) * df_da:(DV * D * D -> DV) * df_db:(DV * DV * DV -> DV) * df_dab:(DV * D * D * DV * DV -> DV) * r_d_d:(D * DV -> TraceOp) * r_d_c:(D * DV -> TraceOp) * r_c_d:(D * DV -> TraceOp) -> DV
static member Pow : a:int * b:DV -> DV
static member Pow : a:DV * b:int -> DV
static member Pow : a:float32 * b:DV -> DV
static member Pow : a:DV * b:float32 -> DV
static member Pow : a:D * b:DV -> DV
static member Pow : a:DV * b:D -> DV
static member Pow : a:DV * b:DV -> DV
static member ReLU : a:DV -> DV
static member ReshapeToDM : m:int * a:DV -> DM
static member Round : a:DV -> DV
static member Sigmoid : a:DV -> DV
static member Sign : a:DV -> DV
static member Sin : a:DV -> DV
static member Sinh : a:DV -> DV
static member SoftMax : a:DV -> DV
static member SoftPlus : a:DV -> DV
static member SoftSign : a:DV -> DV
static member Split : d:DV * n:seq<int> -> seq<DV>
static member Sqrt : a:DV -> DV
static member StandardDev : a:DV -> D
static member Standardize : a:DV -> DV
static member Sum : a:DV -> D
static member Tan : a:DV -> DV
static member Tanh : a:DV -> DV
static member Variance : a:DV -> D
static member ZeroN : n:int -> DV
static member Zero : DV
static member ( + ) : a:int * b:DV -> DV
static member ( + ) : a:DV * b:int -> DV
static member ( + ) : a:float32 * b:DV -> DV
static member ( + ) : a:DV * b:float32 -> DV
static member ( + ) : a:D * b:DV -> DV
static member ( + ) : a:DV * b:D -> DV
static member ( + ) : a:DV * b:DV -> DV
static member ( &* ) : a:DV * b:DV -> DM
static member ( / ) : a:int * b:DV -> DV
static member ( / ) : a:DV * b:int -> DV
static member ( / ) : a:float32 * b:DV -> DV
static member ( / ) : a:DV * b:float32 -> DV
static member ( / ) : a:D * b:DV -> DV
static member ( / ) : a:DV * b:D -> DV
static member ( ./ ) : a:DV * b:DV -> DV
static member ( .* ) : a:DV * b:DV -> DV
static member op_Explicit : d:float32 [] -> DV
static member op_Explicit : d:DV -> float32 []
static member ( * ) : a:int * b:DV -> DV
static member ( * ) : a:DV * b:int -> DV
static member ( * ) : a:float32 * b:DV -> DV
static member ( * ) : a:DV * b:float32 -> DV
static member ( * ) : a:D * b:DV -> DV
static member ( * ) : a:DV * b:D -> DV
static member ( * ) : a:DV * b:DV -> D
static member ( - ) : a:int * b:DV -> DV
static member ( - ) : a:DV * b:int -> DV
static member ( - ) : a:float32 * b:DV -> DV
static member ( - ) : a:DV * b:float32 -> DV
static member ( - ) : a:D * b:DV -> DV
static member ( - ) : a:DV * b:D -> DV
static member ( - ) : a:DV * b:DV -> DV
static member ( ~- ) : a:DV -> DV
Full name: DiffSharp.AD.Float32.DV
union case DV.DV: float32 [] -> DV
--------------------
module DV
from DiffSharp.AD.Float32
--------------------
type DV =
| DV of float32 []
| DVF of DV * DV * uint32
| DVR of DV * DV ref * TraceOp * uint32 ref * uint32
member Copy : unit -> DV
member GetForward : t:DV * i:uint32 -> DV
member GetReverse : i:uint32 -> DV
member GetSlice : lower:int option * upper:int option -> DV
member ToArray : unit -> D []
member ToColDM : unit -> DM
member ToMathematicaString : unit -> string
member ToMatlabString : unit -> string
member ToRowDM : unit -> DM
override ToString : unit -> string
member Visualize : unit -> string
member A : DV
member F : uint32
member Item : i:int -> D with get
member Length : int
member P : DV
member PD : DV
member T : DV
member A : DV with set
member F : uint32 with set
static member Abs : a:DV -> DV
static member Acos : a:DV -> DV
static member AddItem : a:DV * i:int * b:D -> DV
static member AddSubVector : a:DV * i:int * b:DV -> DV
static member Append : a:DV * b:DV -> DV
static member Asin : a:DV -> DV
static member Atan : a:DV -> DV
static member Atan2 : a:int * b:DV -> DV
static member Atan2 : a:DV * b:int -> DV
static member Atan2 : a:float32 * b:DV -> DV
static member Atan2 : a:DV * b:float32 -> DV
static member Atan2 : a:D * b:DV -> DV
static member Atan2 : a:DV * b:D -> DV
static member Atan2 : a:DV * b:DV -> DV
static member Ceiling : a:DV -> DV
static member Cos : a:DV -> DV
static member Cosh : a:DV -> DV
static member Exp : a:DV -> DV
static member Floor : a:DV -> DV
static member L1Norm : a:DV -> D
static member L2Norm : a:DV -> D
static member L2NormSq : a:DV -> D
static member Log : a:DV -> DV
static member Log10 : a:DV -> DV
static member LogSumExp : a:DV -> D
static member Max : a:DV -> D
static member Max : a:D * b:DV -> DV
static member Max : a:DV * b:D -> DV
static member Max : a:DV * b:DV -> DV
static member MaxIndex : a:DV -> int
static member Mean : a:DV -> D
static member Min : a:DV -> D
static member Min : a:D * b:DV -> DV
static member Min : a:DV * b:D -> DV
static member Min : a:DV * b:DV -> DV
static member MinIndex : a:DV -> int
static member Normalize : a:DV -> DV
static member OfArray : a:D [] -> DV
static member Op_DV_D : a:DV * ff:(float32 [] -> float32) * fd:(DV -> D) * df:(D * DV * DV -> D) * r:(DV -> TraceOp) -> D
static member Op_DV_DM : a:DV * ff:(float32 [] -> float32 [,]) * fd:(DV -> DM) * df:(DM * DV * DV -> DM) * r:(DV -> TraceOp) -> DM
static member Op_DV_DV : a:DV * ff:(float32 [] -> float32 []) * fd:(DV -> DV) * df:(DV * DV * DV -> DV) * r:(DV -> TraceOp) -> DV
static member Op_DV_DV_D : a:DV * b:DV * ff:(float32 [] * float32 [] -> float32) * fd:(DV * DV -> D) * df_da:(D * DV * DV -> D) * df_db:(D * DV * DV -> D) * df_dab:(D * DV * DV * DV * DV -> D) * r_d_d:(DV * DV -> TraceOp) * r_d_c:(DV * DV -> TraceOp) * r_c_d:(DV * DV -> TraceOp) -> D
static member Op_DV_DV_DM : a:DV * b:DV * ff:(float32 [] * float32 [] -> float32 [,]) * fd:(DV * DV -> DM) * df_da:(DM * DV * DV -> DM) * df_db:(DM * DV * DV -> DM) * df_dab:(DM * DV * DV * DV * DV -> DM) * r_d_d:(DV * DV -> TraceOp) * r_d_c:(DV * DV -> TraceOp) * r_c_d:(DV * DV -> TraceOp) -> DM
static member Op_DV_DV_DV : a:DV * b:DV * ff:(float32 [] * float32 [] -> float32 []) * fd:(DV * DV -> DV) * df_da:(DV * DV * DV -> DV) * df_db:(DV * DV * DV -> DV) * df_dab:(DV * DV * DV * DV * DV -> DV) * r_d_d:(DV * DV -> TraceOp) * r_d_c:(DV * DV -> TraceOp) * r_c_d:(DV * DV -> TraceOp) -> DV
static member Op_DV_D_DV : a:DV * b:D * ff:(float32 [] * float32 -> float32 []) * fd:(DV * D -> DV) * df_da:(DV * DV * DV -> DV) * df_db:(DV * D * D -> DV) * df_dab:(DV * DV * DV * D * D -> DV) * r_d_d:(DV * D -> TraceOp) * r_d_c:(DV * D -> TraceOp) * r_c_d:(DV * D -> TraceOp) -> DV
static member Op_D_DV_DV : a:D * b:DV * ff:(float32 * float32 [] -> float32 []) * fd:(D * DV -> DV) * df_da:(DV * D * D -> DV) * df_db:(DV * DV * DV -> DV) * df_dab:(DV * D * D * DV * DV -> DV) * r_d_d:(D * DV -> TraceOp) * r_d_c:(D * DV -> TraceOp) * r_c_d:(D * DV -> TraceOp) -> DV
static member Pow : a:int * b:DV -> DV
static member Pow : a:DV * b:int -> DV
static member Pow : a:float32 * b:DV -> DV
static member Pow : a:DV * b:float32 -> DV
static member Pow : a:D * b:DV -> DV
static member Pow : a:DV * b:D -> DV
static member Pow : a:DV * b:DV -> DV
static member ReLU : a:DV -> DV
static member ReshapeToDM : m:int * a:DV -> DM
static member Round : a:DV -> DV
static member Sigmoid : a:DV -> DV
static member Sign : a:DV -> DV
static member Sin : a:DV -> DV
static member Sinh : a:DV -> DV
static member SoftMax : a:DV -> DV
static member SoftPlus : a:DV -> DV
static member SoftSign : a:DV -> DV
static member Split : d:DV * n:seq<int> -> seq<DV>
static member Sqrt : a:DV -> DV
static member StandardDev : a:DV -> D
static member Standardize : a:DV -> DV
static member Sum : a:DV -> D
static member Tan : a:DV -> DV
static member Tanh : a:DV -> DV
static member Variance : a:DV -> D
static member ZeroN : n:int -> DV
static member Zero : DV
static member ( + ) : a:int * b:DV -> DV
static member ( + ) : a:DV * b:int -> DV
static member ( + ) : a:float32 * b:DV -> DV
static member ( + ) : a:DV * b:float32 -> DV
static member ( + ) : a:D * b:DV -> DV
static member ( + ) : a:DV * b:D -> DV
static member ( + ) : a:DV * b:DV -> DV
static member ( &* ) : a:DV * b:DV -> DM
static member ( / ) : a:int * b:DV -> DV
static member ( / ) : a:DV * b:int -> DV
static member ( / ) : a:float32 * b:DV -> DV
static member ( / ) : a:DV * b:float32 -> DV
static member ( / ) : a:D * b:DV -> DV
static member ( / ) : a:DV * b:D -> DV
static member ( ./ ) : a:DV * b:DV -> DV
static member ( .* ) : a:DV * b:DV -> DV
static member op_Explicit : d:float32 [] -> DV
static member op_Explicit : d:DV -> float32 []
static member ( * ) : a:int * b:DV -> DV
static member ( * ) : a:DV * b:int -> DV
static member ( * ) : a:float32 * b:DV -> DV
static member ( * ) : a:DV * b:float32 -> DV
static member ( * ) : a:D * b:DV -> DV
static member ( * ) : a:DV * b:D -> DV
static member ( * ) : a:DV * b:DV -> D
static member ( - ) : a:int * b:DV -> DV
static member ( - ) : a:DV * b:int -> DV
static member ( - ) : a:float32 * b:DV -> DV
static member ( - ) : a:DV * b:float32 -> DV
static member ( - ) : a:D * b:DV -> DV
static member ( - ) : a:DV * b:D -> DV
static member ( - ) : a:DV * b:DV -> DV
static member ( ~- ) : a:DV -> DV
Full name: DiffSharp.AD.Float32.DV
val x : DV
val wopt : DV
Full name: Training.wopt
Full name: Training.wopt
val lopt : D
Full name: Training.lopt
Full name: Training.lopt
val whist : DV []
Full name: Training.whist
Full name: Training.whist
val lhist : D []
Full name: Training.lhist
Full name: Training.lhist
type Optimize =
static member Minimize : f:(DV -> D) * w0:DV -> DV * D * DV [] * D []
static member Minimize : f:(DV -> D) * w0:DV * par:Params -> DV * D * DV [] * D []
static member Train : f:(DV -> DM -> DM) * w0:DV * d:Dataset -> DV * D * DV [] * D []
static member Train : f:(DV -> DV -> DV) * w0:DV * d:Dataset -> DV * D * DV [] * D []
static member Train : f:(DV -> DV -> D) * w0:DV * d:Dataset -> DV * D * DV [] * D []
static member Train : f:(DV -> DM -> DM) * w0:DV * d:Dataset * v:Dataset -> DV * D * DV [] * D []
static member Train : f:(DV -> DM -> DM) * w0:DV * d:Dataset * par:Params -> DV * D * DV [] * D []
static member Train : f:(DV -> DV -> DV) * w0:DV * d:Dataset * v:Dataset -> DV * D * DV [] * D []
static member Train : f:(DV -> DV -> DV) * w0:DV * d:Dataset * par:Params -> DV * D * DV [] * D []
static member Train : f:(DV -> DV -> D) * w0:DV * d:Dataset * v:Dataset -> DV * D * DV [] * D []
...
Full name: Hype.Optimize
static member Minimize : f:(DV -> D) * w0:DV -> DV * D * DV [] * D []
static member Minimize : f:(DV -> D) * w0:DV * par:Params -> DV * D * DV [] * D []
static member Train : f:(DV -> DM -> DM) * w0:DV * d:Dataset -> DV * D * DV [] * D []
static member Train : f:(DV -> DV -> DV) * w0:DV * d:Dataset -> DV * D * DV [] * D []
static member Train : f:(DV -> DV -> D) * w0:DV * d:Dataset -> DV * D * DV [] * D []
static member Train : f:(DV -> DM -> DM) * w0:DV * d:Dataset * v:Dataset -> DV * D * DV [] * D []
static member Train : f:(DV -> DM -> DM) * w0:DV * d:Dataset * par:Params -> DV * D * DV [] * D []
static member Train : f:(DV -> DV -> DV) * w0:DV * d:Dataset * v:Dataset -> DV * D * DV [] * D []
static member Train : f:(DV -> DV -> DV) * w0:DV * d:Dataset * par:Params -> DV * D * DV [] * D []
static member Train : f:(DV -> DV -> D) * w0:DV * d:Dataset * v:Dataset -> DV * D * DV [] * D []
...
Full name: Hype.Optimize
static member Optimize.Train : f:(DV -> DM -> DM) * w0:DV * d:Dataset -> DV * D * DV [] * D []
(+0 other overloads)
static member Optimize.Train : f:(DV -> DV -> DV) * w0:DV * d:Dataset -> DV * D * DV [] * D []
(+0 other overloads)
static member Optimize.Train : f:(DV -> DV -> D) * w0:DV * d:Dataset -> DV * D * DV [] * D []
(+0 other overloads)
static member Optimize.Train : f:(DV -> DM -> DM) * w0:DV * d:Dataset * v:Dataset -> DV * D * DV [] * D []
(+0 other overloads)
static member Optimize.Train : f:(DV -> DM -> DM) * w0:DV * d:Dataset * par:Params -> DV * D * DV [] * D []
(+0 other overloads)
static member Optimize.Train : f:(DV -> DV -> DV) * w0:DV * d:Dataset * v:Dataset -> DV * D * DV [] * D []
(+0 other overloads)
static member Optimize.Train : f:(DV -> DV -> DV) * w0:DV * d:Dataset * par:Params -> DV * D * DV [] * D []
(+0 other overloads)
static member Optimize.Train : f:(DV -> DV -> D) * w0:DV * d:Dataset * v:Dataset -> DV * D * DV [] * D []
(+0 other overloads)
static member Optimize.Train : f:(DV -> DV -> D) * w0:DV * d:Dataset * par:Params -> DV * D * DV [] * D []
(+0 other overloads)
static member Optimize.Train : f:(DV -> DM -> DM) * w0:DV * d:Dataset * v:Dataset * par:Params -> DV * D * DV [] * D []
(+0 other overloads)
(+0 other overloads)
static member Optimize.Train : f:(DV -> DV -> DV) * w0:DV * d:Dataset -> DV * D * DV [] * D []
(+0 other overloads)
static member Optimize.Train : f:(DV -> DV -> D) * w0:DV * d:Dataset -> DV * D * DV [] * D []
(+0 other overloads)
static member Optimize.Train : f:(DV -> DM -> DM) * w0:DV * d:Dataset * v:Dataset -> DV * D * DV [] * D []
(+0 other overloads)
static member Optimize.Train : f:(DV -> DM -> DM) * w0:DV * d:Dataset * par:Params -> DV * D * DV [] * D []
(+0 other overloads)
static member Optimize.Train : f:(DV -> DV -> DV) * w0:DV * d:Dataset * v:Dataset -> DV * D * DV [] * D []
(+0 other overloads)
static member Optimize.Train : f:(DV -> DV -> DV) * w0:DV * d:Dataset * par:Params -> DV * D * DV [] * D []
(+0 other overloads)
static member Optimize.Train : f:(DV -> DV -> D) * w0:DV * d:Dataset * v:Dataset -> DV * D * DV [] * D []
(+0 other overloads)
static member Optimize.Train : f:(DV -> DV -> D) * w0:DV * d:Dataset * par:Params -> DV * D * DV [] * D []
(+0 other overloads)
static member Optimize.Train : f:(DV -> DM -> DM) * w0:DV * d:Dataset * v:Dataset * par:Params -> DV * D * DV [] * D []
(+0 other overloads)
Multiple items
type Rnd =
new : unit -> Rnd
static member Choice : a:'a0 [] -> 'a0
static member Choice : a:'a [] * probs:DV -> 'a
static member Choice : a:'a0 [] * probs:float32 [] -> 'a0
static member Normal : unit -> float32
static member Normal : mu:float32 * sigma:float32 -> float32
static member NormalD : unit -> D
static member NormalD : mu:D * sigma:D -> D
static member NormalDM : m:int * n:int -> DM
static member NormalDM : m:int * n:int * mu:D * sigma:D -> DM
...
Full name: Hype.Rnd
--------------------
new : unit -> Rnd
type Rnd =
new : unit -> Rnd
static member Choice : a:'a0 [] -> 'a0
static member Choice : a:'a [] * probs:DV -> 'a
static member Choice : a:'a0 [] * probs:float32 [] -> 'a0
static member Normal : unit -> float32
static member Normal : mu:float32 * sigma:float32 -> float32
static member NormalD : unit -> D
static member NormalD : mu:D * sigma:D -> D
static member NormalDM : m:int * n:int -> DM
static member NormalDM : m:int * n:int * mu:D * sigma:D -> DM
...
Full name: Hype.Rnd
--------------------
new : unit -> Rnd
static member Rnd.UniformDV : n:int -> DV
static member Rnd.UniformDV : n:int * max:D -> DV
static member Rnd.UniformDV : n:int * min:D * max:D -> DV
static member Rnd.UniformDV : n:int * max:D -> DV
static member Rnd.UniformDV : n:int * min:D * max:D -> DV
Multiple items
module Params
from Hype
--------------------
type Params =
{Epochs: int;
Method: Method;
LearningRate: LearningRate;
Momentum: Momentum;
Loss: Loss;
Regularization: Regularization;
GradientClipping: GradientClipping;
Batch: Batch;
EarlyStopping: EarlyStopping;
ImprovementThreshold: D;
...}
Full name: Hype.Params
module Params
from Hype
--------------------
type Params =
{Epochs: int;
Method: Method;
LearningRate: LearningRate;
Momentum: Momentum;
Loss: Loss;
Regularization: Regularization;
GradientClipping: GradientClipping;
Batch: Batch;
EarlyStopping: EarlyStopping;
ImprovementThreshold: D;
...}
Full name: Hype.Params
val Default : Params
Full name: Hype.Params.Default
Full name: Hype.Params.Default
type Loss =
| L1Loss
| L2Loss
| Quadratic
| CrossEntropyOnLinear
| CrossEntropyOnSoftmax
override ToString : unit -> string
member Func : (Dataset -> (DM -> DM) -> D)
Full name: Hype.Loss
| L1Loss
| L2Loss
| Quadratic
| CrossEntropyOnLinear
| CrossEntropyOnSoftmax
override ToString : unit -> string
member Func : (Dataset -> (DM -> DM) -> D)
Full name: Hype.Loss
union case Loss.Quadratic: Loss
val trainedmodel : (DV -> D)
Full name: Training.trainedmodel
Full name: Training.trainedmodel
namespace RProvider
namespace RProvider.graphics
namespace RProvider.grDevices
val px : float []
Full name: Training.px
Full name: Training.px
val py : float []
Full name: Training.py
Full name: Training.py
property Dataset.Y: DM
val toArray : v:DV -> D []
Full name: DiffSharp.AD.Float32.DV.toArray
Full name: DiffSharp.AD.Float32.DV.toArray
module Array
from Microsoft.FSharp.Collections
from Microsoft.FSharp.Collections
val mapi : mapping:(int -> 'T -> 'U) -> array:'T [] -> 'U []
Full name: Microsoft.FSharp.Collections.Array.mapi
Full name: Microsoft.FSharp.Collections.Array.mapi
val i : int
val v : D
Multiple items
val float : value:'T -> float (requires member op_Explicit)
Full name: Microsoft.FSharp.Core.Operators.float
--------------------
type float = System.Double
Full name: Microsoft.FSharp.Core.float
--------------------
type float<'Measure> = float
Full name: Microsoft.FSharp.Core.float<_>
val float : value:'T -> float (requires member op_Explicit)
Full name: Microsoft.FSharp.Core.Operators.float
--------------------
type float = System.Double
Full name: Microsoft.FSharp.Core.float
--------------------
type float<'Measure> = float
Full name: Microsoft.FSharp.Core.float<_>
Multiple items
val float32 : value:'T -> float32 (requires member op_Explicit)
Full name: Microsoft.FSharp.Core.Operators.float32
--------------------
type float32 = System.Single
Full name: Microsoft.FSharp.Core.float32
--------------------
type float32<'Measure> = float32
Full name: Microsoft.FSharp.Core.float32<_>
val float32 : value:'T -> float32 (requires member op_Explicit)
Full name: Microsoft.FSharp.Core.Operators.float32
--------------------
type float32 = System.Single
Full name: Microsoft.FSharp.Core.float32
--------------------
type float32<'Measure> = float32
Full name: Microsoft.FSharp.Core.float32<_>
val unzip : array:('T1 * 'T2) [] -> 'T1 [] * 'T2 []
Full name: Microsoft.FSharp.Collections.Array.unzip
Full name: Microsoft.FSharp.Collections.Array.unzip
val ppx : float []
Full name: Training.ppx
Full name: Training.ppx
val ppy : float []
Full name: Training.ppy
Full name: Training.ppy
property Dataset.X: DM
val mapCols : f:(DV -> DV) -> m:DM -> DM
Full name: DiffSharp.AD.Float32.DM.mapCols
Full name: DiffSharp.AD.Float32.DM.mapCols
val v : DV
val toDV : m:DM -> DV
Full name: DiffSharp.AD.Float32.DM.toDV
Full name: DiffSharp.AD.Float32.DM.toDV
val ll : float []
Full name: Training.ll
Full name: Training.ll
val map : mapping:('T -> 'U) -> array:'T [] -> 'U []
Full name: Microsoft.FSharp.Collections.Array.map
Full name: Microsoft.FSharp.Collections.Array.map
val namedParams : s:seq<string * 'a> -> System.Collections.Generic.IDictionary<string,obj>
Full name: RProvider.Helpers.namedParams
Full name: RProvider.Helpers.namedParams
val box : value:'T -> obj
Full name: Microsoft.FSharp.Core.Operators.box
Full name: Microsoft.FSharp.Core.Operators.box
type R =
static member Axis : ?x: obj * ?at: obj * ?___: obj * ?side: obj * ?labels: obj * ?paramArray: obj [] -> SymbolicExpression + 1 overload
static member abline : ?a: obj * ?b: obj * ?h: obj * ?v: obj * ?reg: obj * ?coef: obj * ?untf: obj * ?___: obj * ?paramArray: obj [] -> SymbolicExpression + 1 overload
static member arrows : ?x0: obj * ?y0: obj * ?x1: obj * ?y1: obj * ?length: obj * ?angle: obj * ?code: obj * ?col: obj * ?lty: obj * ?lwd: obj * ?___: obj * ?paramArray: obj [] -> SymbolicExpression + 1 overload
static member assocplot : ?x: obj * ?col: obj * ?space: obj * ?main: obj * ?xlab: obj * ?ylab: obj -> SymbolicExpression + 1 overload
static member axTicks : ?side: obj * ?axp: obj * ?usr: obj * ?log: obj * ?nintLog: obj -> SymbolicExpression + 1 overload
static member axis : ?side: obj * ?at: obj * ?labels: obj * ?tick: obj * ?line: obj * ?pos: obj * ?outer: obj * ?font: obj * ?lty: obj * ?lwd: obj * ?lwd_ticks: obj * ?col: obj * ?col_ticks: obj * ?hadj: obj * ?padj: obj * ?___: obj * ?paramArray: obj [] -> SymbolicExpression + 1 overload
static member axis_Date : ?side: obj * ?x: obj * ?at: obj * ?format: obj * ?labels: obj * ?___: obj * ?paramArray: obj [] -> SymbolicExpression + 1 overload
static member axis_POSIXct : ?side: obj * ?x: obj * ?at: obj * ?format: obj * ?labels: obj * ?___: obj * ?paramArray: obj [] -> SymbolicExpression + 1 overload
static member barplot : ?height: obj * ?___: obj * ?paramArray: obj [] -> SymbolicExpression + 1 overload
static member barplot_default : ?height: obj * ?width: obj * ?space: obj * ?names_arg: obj * ?legend_text: obj * ?beside: obj * ?horiz: obj * ?density: obj * ?angle: obj * ?col: obj * ?border: obj * ?main: obj * ?sub: obj * ?xlab: obj * ?ylab: obj * ?xlim: obj * ?ylim: obj * ?xpd: obj * ?log: obj * ?axes: obj * ?axisnames: obj * ?cex_axis: obj * ?cex_names: obj * ?inside: obj * ?plot: obj * ?axis_lty: obj * ?offset: obj * ?add: obj * ?args_legend: obj * ?___: obj * ?paramArray: obj [] -> SymbolicExpression + 1 overload
...
Full name: RProvider.graphics.R
R functions for base graphics
static member Axis : ?x: obj * ?at: obj * ?___: obj * ?side: obj * ?labels: obj * ?paramArray: obj [] -> SymbolicExpression + 1 overload
static member abline : ?a: obj * ?b: obj * ?h: obj * ?v: obj * ?reg: obj * ?coef: obj * ?untf: obj * ?___: obj * ?paramArray: obj [] -> SymbolicExpression + 1 overload
static member arrows : ?x0: obj * ?y0: obj * ?x1: obj * ?y1: obj * ?length: obj * ?angle: obj * ?code: obj * ?col: obj * ?lty: obj * ?lwd: obj * ?___: obj * ?paramArray: obj [] -> SymbolicExpression + 1 overload
static member assocplot : ?x: obj * ?col: obj * ?space: obj * ?main: obj * ?xlab: obj * ?ylab: obj -> SymbolicExpression + 1 overload
static member axTicks : ?side: obj * ?axp: obj * ?usr: obj * ?log: obj * ?nintLog: obj -> SymbolicExpression + 1 overload
static member axis : ?side: obj * ?at: obj * ?labels: obj * ?tick: obj * ?line: obj * ?pos: obj * ?outer: obj * ?font: obj * ?lty: obj * ?lwd: obj * ?lwd_ticks: obj * ?col: obj * ?col_ticks: obj * ?hadj: obj * ?padj: obj * ?___: obj * ?paramArray: obj [] -> SymbolicExpression + 1 overload
static member axis_Date : ?side: obj * ?x: obj * ?at: obj * ?format: obj * ?labels: obj * ?___: obj * ?paramArray: obj [] -> SymbolicExpression + 1 overload
static member axis_POSIXct : ?side: obj * ?x: obj * ?at: obj * ?format: obj * ?labels: obj * ?___: obj * ?paramArray: obj [] -> SymbolicExpression + 1 overload
static member barplot : ?height: obj * ?___: obj * ?paramArray: obj [] -> SymbolicExpression + 1 overload
static member barplot_default : ?height: obj * ?width: obj * ?space: obj * ?names_arg: obj * ?legend_text: obj * ?beside: obj * ?horiz: obj * ?density: obj * ?angle: obj * ?col: obj * ?border: obj * ?main: obj * ?sub: obj * ?xlab: obj * ?ylab: obj * ?xlim: obj * ?ylim: obj * ?xpd: obj * ?log: obj * ?axes: obj * ?axisnames: obj * ?cex_axis: obj * ?cex_names: obj * ?inside: obj * ?plot: obj * ?axis_lty: obj * ?offset: obj * ?add: obj * ?args_legend: obj * ?___: obj * ?paramArray: obj [] -> SymbolicExpression + 1 overload
...
Full name: RProvider.graphics.R
R functions for base graphics
R.plot(paramsByName: System.Collections.Generic.IDictionary<string,obj>) : RDotNet.SymbolicExpression
R.plot(?x: obj, ?y: obj, ?___: obj, ?paramArray: obj []) : RDotNet.SymbolicExpression
Generic X-Y Plotting
R.plot(?x: obj, ?y: obj, ?___: obj, ?paramArray: obj []) : RDotNet.SymbolicExpression
Generic X-Y Plotting
val ignore : value:'T -> unit
Full name: Microsoft.FSharp.Core.Operators.ignore
Full name: Microsoft.FSharp.Core.Operators.ignore
R.points(paramsByName: System.Collections.Generic.IDictionary<string,obj>) : RDotNet.SymbolicExpression
R.points(?x: obj, ?___: obj, ?paramArray: obj []) : RDotNet.SymbolicExpression
Add Points to a Plot
R.points(?x: obj, ?___: obj, ?paramArray: obj []) : RDotNet.SymbolicExpression
Add Points to a Plot
type Loss =
| L1Loss
| L2Loss
| Quadratic
| CrossEntropyOnLinear
| CrossEntropyOnSoftmax
Full name: Training.Loss
| L1Loss
| L2Loss
| Quadratic
| CrossEntropyOnLinear
| CrossEntropyOnSoftmax
Full name: Training.Loss
union case Loss.L1Loss: Loss
union case Loss.L2Loss: Loss
union case Loss.CrossEntropyOnLinear: Loss
union case Loss.CrossEntropyOnSoftmax: Loss
type Regularization =
| L1Reg of D
| L2Reg of D
| NoReg
static member DefaultL1Reg : Regularization
static member DefaultL2Reg : Regularization
Full name: Training.Regularization
| L1Reg of D
| L2Reg of D
| NoReg
static member DefaultL1Reg : Regularization
static member DefaultL2Reg : Regularization
Full name: Training.Regularization
union case Regularization.L1Reg: D -> Regularization
type D =
| D of float32
| DF of D * D * uint32
| DR of D * D ref * TraceOp * uint32 ref * uint32
interface IComparable
member Copy : unit -> D
override Equals : other:obj -> bool
member GetForward : t:D * i:uint32 -> D
override GetHashCode : unit -> int
member GetReverse : i:uint32 -> D
override ToString : unit -> string
member A : D
member F : uint32
member P : D
member PD : D
member T : D
member A : D with set
member F : uint32 with set
static member Abs : a:D -> D
static member Acos : a:D -> D
static member Asin : a:D -> D
static member Atan : a:D -> D
static member Atan2 : a:int * b:D -> D
static member Atan2 : a:D * b:int -> D
static member Atan2 : a:float32 * b:D -> D
static member Atan2 : a:D * b:float32 -> D
static member Atan2 : a:D * b:D -> D
static member Ceiling : a:D -> D
static member Cos : a:D -> D
static member Cosh : a:D -> D
static member Exp : a:D -> D
static member Floor : a:D -> D
static member Log : a:D -> D
static member Log10 : a:D -> D
static member LogSumExp : a:D -> D
static member Max : a:D * b:D -> D
static member Min : a:D * b:D -> D
static member Op_D_D : a:D * ff:(float32 -> float32) * fd:(D -> D) * df:(D * D * D -> D) * r:(D -> TraceOp) -> D
static member Op_D_D_D : a:D * b:D * ff:(float32 * float32 -> float32) * fd:(D * D -> D) * df_da:(D * D * D -> D) * df_db:(D * D * D -> D) * df_dab:(D * D * D * D * D -> D) * r_d_d:(D * D -> TraceOp) * r_d_c:(D * D -> TraceOp) * r_c_d:(D * D -> TraceOp) -> D
static member Pow : a:int * b:D -> D
static member Pow : a:D * b:int -> D
static member Pow : a:float32 * b:D -> D
static member Pow : a:D * b:float32 -> D
static member Pow : a:D * b:D -> D
static member ReLU : a:D -> D
static member Round : a:D -> D
static member Sigmoid : a:D -> D
static member Sign : a:D -> D
static member Sin : a:D -> D
static member Sinh : a:D -> D
static member SoftPlus : a:D -> D
static member SoftSign : a:D -> D
static member Sqrt : a:D -> D
static member Tan : a:D -> D
static member Tanh : a:D -> D
static member One : D
static member Zero : D
static member ( + ) : a:int * b:D -> D
static member ( + ) : a:D * b:int -> D
static member ( + ) : a:float32 * b:D -> D
static member ( + ) : a:D * b:float32 -> D
static member ( + ) : a:D * b:D -> D
static member ( / ) : a:int * b:D -> D
static member ( / ) : a:D * b:int -> D
static member ( / ) : a:float32 * b:D -> D
static member ( / ) : a:D * b:float32 -> D
static member ( / ) : a:D * b:D -> D
static member op_Explicit : d:D -> float32
static member ( * ) : a:int * b:D -> D
static member ( * ) : a:D * b:int -> D
static member ( * ) : a:float32 * b:D -> D
static member ( * ) : a:D * b:float32 -> D
static member ( * ) : a:D * b:D -> D
static member ( - ) : a:int * b:D -> D
static member ( - ) : a:D * b:int -> D
static member ( - ) : a:float32 * b:D -> D
static member ( - ) : a:D * b:float32 -> D
static member ( - ) : a:D * b:D -> D
static member ( ~- ) : a:D -> D
Full name: DiffSharp.AD.Float32.D
| D of float32
| DF of D * D * uint32
| DR of D * D ref * TraceOp * uint32 ref * uint32
interface IComparable
member Copy : unit -> D
override Equals : other:obj -> bool
member GetForward : t:D * i:uint32 -> D
override GetHashCode : unit -> int
member GetReverse : i:uint32 -> D
override ToString : unit -> string
member A : D
member F : uint32
member P : D
member PD : D
member T : D
member A : D with set
member F : uint32 with set
static member Abs : a:D -> D
static member Acos : a:D -> D
static member Asin : a:D -> D
static member Atan : a:D -> D
static member Atan2 : a:int * b:D -> D
static member Atan2 : a:D * b:int -> D
static member Atan2 : a:float32 * b:D -> D
static member Atan2 : a:D * b:float32 -> D
static member Atan2 : a:D * b:D -> D
static member Ceiling : a:D -> D
static member Cos : a:D -> D
static member Cosh : a:D -> D
static member Exp : a:D -> D
static member Floor : a:D -> D
static member Log : a:D -> D
static member Log10 : a:D -> D
static member LogSumExp : a:D -> D
static member Max : a:D * b:D -> D
static member Min : a:D * b:D -> D
static member Op_D_D : a:D * ff:(float32 -> float32) * fd:(D -> D) * df:(D * D * D -> D) * r:(D -> TraceOp) -> D
static member Op_D_D_D : a:D * b:D * ff:(float32 * float32 -> float32) * fd:(D * D -> D) * df_da:(D * D * D -> D) * df_db:(D * D * D -> D) * df_dab:(D * D * D * D * D -> D) * r_d_d:(D * D -> TraceOp) * r_d_c:(D * D -> TraceOp) * r_c_d:(D * D -> TraceOp) -> D
static member Pow : a:int * b:D -> D
static member Pow : a:D * b:int -> D
static member Pow : a:float32 * b:D -> D
static member Pow : a:D * b:float32 -> D
static member Pow : a:D * b:D -> D
static member ReLU : a:D -> D
static member Round : a:D -> D
static member Sigmoid : a:D -> D
static member Sign : a:D -> D
static member Sin : a:D -> D
static member Sinh : a:D -> D
static member SoftPlus : a:D -> D
static member SoftSign : a:D -> D
static member Sqrt : a:D -> D
static member Tan : a:D -> D
static member Tanh : a:D -> D
static member One : D
static member Zero : D
static member ( + ) : a:int * b:D -> D
static member ( + ) : a:D * b:int -> D
static member ( + ) : a:float32 * b:D -> D
static member ( + ) : a:D * b:float32 -> D
static member ( + ) : a:D * b:D -> D
static member ( / ) : a:int * b:D -> D
static member ( / ) : a:D * b:int -> D
static member ( / ) : a:float32 * b:D -> D
static member ( / ) : a:D * b:float32 -> D
static member ( / ) : a:D * b:D -> D
static member op_Explicit : d:D -> float32
static member ( * ) : a:int * b:D -> D
static member ( * ) : a:D * b:int -> D
static member ( * ) : a:float32 * b:D -> D
static member ( * ) : a:D * b:float32 -> D
static member ( * ) : a:D * b:D -> D
static member ( - ) : a:int * b:D -> D
static member ( - ) : a:D * b:int -> D
static member ( - ) : a:float32 * b:D -> D
static member ( - ) : a:D * b:float32 -> D
static member ( - ) : a:D * b:D -> D
static member ( ~- ) : a:D -> D
Full name: DiffSharp.AD.Float32.D
union case Regularization.L2Reg: D -> Regularization
union case Regularization.NoReg: Regularization
static member Regularization.DefaultL1Reg : Regularization
Full name: Training.Regularization.DefaultL1Reg
Full name: Training.Regularization.DefaultL1Reg
union case D.D: float32 -> D
static member Regularization.DefaultL2Reg : Regularization
Full name: Training.Regularization.DefaultL2Reg
Full name: Training.Regularization.DefaultL2Reg
type Batch =
| Full
| Minibatch of int
| Stochastic
Full name: Training.Batch
| Full
| Minibatch of int
| Stochastic
Full name: Training.Batch
union case Batch.Full: Batch
union case Batch.Minibatch: int -> Batch
Multiple items
val int : value:'T -> int (requires member op_Explicit)
Full name: Microsoft.FSharp.Core.Operators.int
--------------------
type int = int32
Full name: Microsoft.FSharp.Core.int
--------------------
type int<'Measure> = int
Full name: Microsoft.FSharp.Core.int<_>
val int : value:'T -> int (requires member op_Explicit)
Full name: Microsoft.FSharp.Core.Operators.int
--------------------
type int = int32
Full name: Microsoft.FSharp.Core.int
--------------------
type int<'Measure> = int
Full name: Microsoft.FSharp.Core.int<_>
union case Batch.Stochastic: Batch
type EarlyStopping =
| Early of int * int
| NoEarly
static member DefaultEarly : EarlyStopping
Full name: Training.EarlyStopping
| Early of int * int
| NoEarly
static member DefaultEarly : EarlyStopping
Full name: Training.EarlyStopping
union case EarlyStopping.Early: int * int -> EarlyStopping
union case EarlyStopping.NoEarly: EarlyStopping
static member EarlyStopping.DefaultEarly : EarlyStopping
Full name: Training.EarlyStopping.DefaultEarly
Full name: Training.EarlyStopping.DefaultEarly
val housingtrain : Dataset
Full name: Training.housingtrain
Full name: Training.housingtrain
val housingvalid : Dataset
Full name: Training.housingvalid
Full name: Training.housingvalid
