Optimization

Hype provides a highly configurable and modular gradient-based optimization functionality. This works similar to many other machine learning libraries.

Here's the novelty:

Thanks to nested AD, gradient-based optimization can be combined with any code, including code which internally takes derivatives of a function to produce its output. In other words, you can optimize the value of a function that is internally optimizing another function, or using derivatives for any other purpose (e.g. running particle simulations, adaptive control), up to any level.

In such a compositional optimization setting, all arising higher-order derivatives are handled for you through nested instantiations of forward and/or reverse AD. In any case, you only need to write your algorithms as usual, only implementing a regular forward algorithm.

Let's explain this through a basic example from the article "Jeffrey Mark Siskind and Barak A. Pearlmutter. Nesting forward-mode AD in a functional framework. Higher Order and Symbolic Computation 21(4):361-76, 2008. doi:10.1007/s10990-008-9037-1", where a parameter of a physics simulation using the gradient of an electric potential is optimized with Newton's method using the Hessian of an error, requiring third-order nesting of derivatives.

Optimizing a physics simulation

Consider a charged particle traveling in a plane with position \(\mathbf{x}(t)\), velocity \(\dot{\mathbf{x}}(t)\), initial position \(\mathbf{x}(0)=(0, 8)\), and initial velocity \(\dot{\mathbf{x}}(0)=(0.75, 0)\). The particle is accelerated by an electric field formed by a pair of repulsive bodies,

\[ p(\mathbf{x}; w) = \| \mathbf{x} - (10, 10 - w)\|^{-1} + \| \mathbf{x} - (10, 0)\|^{-1}\]

where \(w\) is a parameter of this simple particle simulation, adjusting the location of one of the repulsive bodies.

We can simulate the time evolution of this system by using a naive Euler ODE integration

\[ \begin{eqnarray*} \ddot{\mathbf{x}}(t) &=& \left. -\nabla_{\mathbf{x}} p(\mathbf{x}) \right|_{\mathbf{x}=\mathbf{x}(t)}\\ \dot{\mathbf{x}}(t + \Delta t) &=& \dot{\mathbf{x}}(t) + \Delta t \ddot{\mathbf{x}}(t)\\ \mathbf{x}(t + \Delta t) &=& \mathbf{x}(t) + \Delta t \dot{\mathbf{x}}(t) \end{eqnarray*}\]

where \(\Delta t\) is an integration time step.

For a given parameter \(w\), the simulation starts with \(t=0\) and finishes when the particle hits the \(x\)-axis, at position \(\mathbf{x}(t_f)\) at time \(t_f\). When the particle hits the \(x\)-axis, we calculate an error \(E(w) = x_0 (t_f)^2\), the squared horizontal distance of the particle from the origin. We then minimize this error using Newton's method, which finds the optimal value of \(w\) so that the particle eventually hits the \(x\)-axis at the origin.

\[ w^{(i+1)} = w^{(i)} - \frac{E'(w^{(i)})}{E''(w^{(i)})}\]

In other words, the code calculating the trajectory of the particle internally computes the gradient of the electric potential \(p(\mathbf{x}; w)\), and, at the same time, the final position of the trajectory \(\mathbf{x}(t_f)\) is used to compute an error, and the gradient and Hessian of this error are computed during the optimization procedure.

Here's how it goes.

 1: 
 2: 
 3: 
 4: 
 5: 
 6: 
 7: 
 8: 
 9: 
10: 
11: 
12: 
13: 
14: 
15: 
16: 
17: 
18: 
19: 
20: 
21: 
22: 
23: 
24: 
25: 
26: 
27: 
28: 
29: 

open Hype
open DiffSharp.AD.Float32

let dt = D 0.1f
let x0 = toDV [0.; 8.]
let v0 = toDV [0.75; 0.]

let p w (x:DV) = (1.f / DV.norm (x - toDV [D 10.f + w * D 0.f; D 10.f - w])) 
               + (1.f / DV.norm (x - toDV [10.; 0.]))

let trajectory (w:D) = 
    (x0, v0) 
    |> Seq.unfold (fun (x, v) ->
                    let a = -grad (p w)  x
                    let v = v + dt * a
                    let x = x + dt * v
                    Some(x, (x, v)))
    |> Seq.takeWhile (fun x -> x.[1] > D 0.f)

let error (w:DV) =
    let xf = trajectory w.[0] |> Seq.last
    xf.[0] * xf.[0]

let w, l, whist, lhist = Optimize.Minimize(error, toDV [0.], 
                                            {Params.Default with 
                                                Method = Newton; 
                                                LearningRate = Constant (D 1.f)
                                                ValidationInterval = 1;
                                                Epochs = 10})

[25/12/2015 23:53:10] --- Minimization started
[25/12/2015 23:53:10] Parameters     : 1
[25/12/2015 23:53:10] Iterations     : 10
[25/12/2015 23:53:10] Valid. interval: 1
[25/12/2015 23:53:10] Method         : Exact Newton
[25/12/2015 23:53:10] Learning rate  : Constant a = D 1.0f
[25/12/2015 23:53:10] Momentum       : None
[25/12/2015 23:53:10] Gradient clip. : None
[25/12/2015 23:53:10] Early stopping : None
[25/12/2015 23:53:10] Improv. thresh.: D 0.995000005f
[25/12/2015 23:53:10] Return best    : true
[25/12/2015 23:53:10]  1/10 | D  2.535113e+000 [- ]
[25/12/2015 23:53:10]  2/10 | D  7.528733e-002 [↓▼]
[25/12/2015 23:53:10]  3/10 | D  1.592970e-002 [↓▼]
[25/12/2015 23:53:10]  4/10 | D  4.178338e-003 [↓▼]
[25/12/2015 23:53:10]  5/10 | D  1.382800e-008 [↓▼]
[25/12/2015 23:53:11]  6/10 | D  3.274181e-011 [↓▼]
[25/12/2015 23:53:11]  7/10 | D  1.151079e-012 [↓▼]
[25/12/2015 23:53:11]  8/10 | D  1.151079e-012 [- ]
[25/12/2015 23:53:11]  9/10 | D  1.151079e-012 [- ]
[25/12/2015 23:53:11] 10/10 | D  3.274181e-011 [↑ ]
[25/12/2015 23:53:11] Duration       : 00:00:00.9201285
[25/12/2015 23:53:11] Value initial  : D  2.535113e+000
[25/12/2015 23:53:11] Value final    : D  1.151079e-012 (Best)
[25/12/2015 23:53:11] Value change   : D -2.535113e+000 (-100.00 %)
[25/12/2015 23:53:11] Value chg. / s : D -2.755173e+000
[25/12/2015 23:53:11] Iter. / s      : 10.86804723
[25/12/2015 23:53:11] Iter. / min    : 652.0828341
[25/12/2015 23:53:11] --- Minimization finished

val whist : DV [] =
  [|DV [|0.0f|]; DV [|0.20767726f|]; DV [|0.17457059f|]; DV [|0.190040559f|];
    DV [|0.182180524f|]; DV [|0.182166189f|]; DV [|0.182166889f|];
    DV [|0.182166755f|]; DV [|0.182166621f|]; DV [|0.182166487f|]|]
val w : DV = DV [|0.182166889f|]
val lhist : D [] =
  [|D 2.5351131f; D 2.5351131f; D 0.0752873272f; D 0.0159297027f;
    D 0.00417833822f; D 1.38279992e-08f; D 3.27418093e-11f; D 1.15107923e-12f;
    D 1.15107923e-12f; D 1.15107923e-12f|]
val l : D = D 1.15107923e-12f

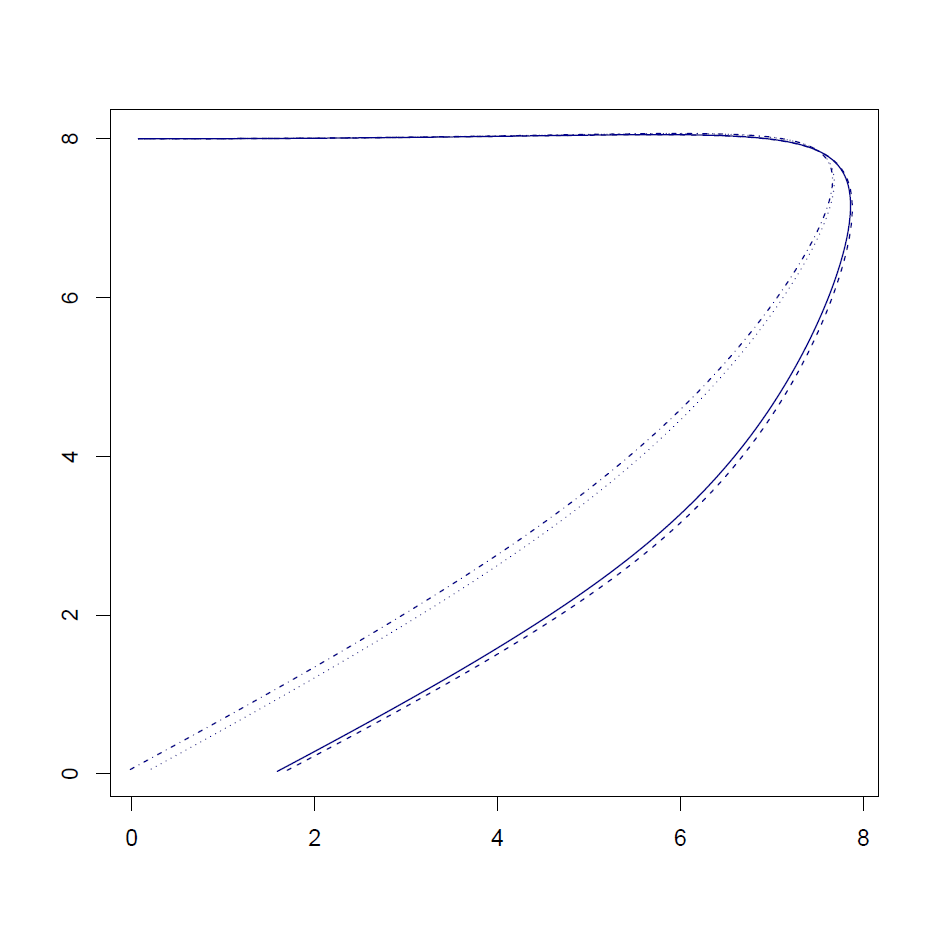
Optimization parameters

As another example, let's optimize the Beale function

\[ f(\mathbf{x}) = (1.5 - x_1 + x_1 x_2)^2 + (2.25 - x_1 + x_1 x_2^2)^2 + (2.625 - x_1 + x_1 x_2^3)^2\]

starting from \(\mathbf{x} = (1, 1.5)\), using RMSProp. The optimum is at \((3, 0.5)\)

1: 
2: 
3: 
4: 
5: 
6: 
7: 
8: 

let beale (x:DV) = (1.5f - x.[0] + (x.[0] * x.[1])) ** 2.f
                    + (2.25f - x.[0] + x.[0] * x.[1] ** 2.f) ** 2.f
                    + (2.625f - x.[0] + x.[0] * x.[1] ** 3.f) ** 2.f

let wopt, lopt, whist, lhist = Optimize.Minimize(beale, toDV [1.; 1.5], 
                                                    {Params.Default with 
                                                        Epochs = 3000; 
                                                        LearningRate = RMSProp (D 0.01f, D 0.9f)})

[12/11/2015 01:22:59] --- Minimization started
[12/11/2015 01:22:59] Parameters     : 2
[12/11/2015 01:22:59] Iterations     : 3000
[12/11/2015 01:22:59] Valid. interval: 10
[12/11/2015 01:22:59] Method         : Gradient descent
[12/11/2015 01:22:59] Learning rate  : RMSProp a0 = D 0.00999999978f, k = D 0.899999976f
[12/11/2015 01:22:59] Momentum       : None
[12/11/2015 01:22:59] Gradient clip. : None
[12/11/2015 01:22:59] Early stopping : None
[12/11/2015 01:22:59] Improv. thresh.: D 0.995000005f
[12/11/2015 01:22:59] Return best    : true
[12/11/2015 01:22:59]    1/3000 | D  4.125000e+001 [- ]
[12/11/2015 01:22:59]   11/3000 | D  2.655878e+001 [↓▼]
[12/11/2015 01:22:59]   21/3000 | D  2.154373e+001 [↓▼]
[12/11/2015 01:22:59]   31/3000 | D  1.841705e+001 [↓▼]
[12/11/2015 01:22:59]   41/3000 | D  1.624916e+001 [↓▼]
[12/11/2015 01:22:59]   51/3000 | D  1.465973e+001 [↓▼]
[12/11/2015 01:22:59]   61/3000 | D  1.334291e+001 [↓▼]
...
[12/11/2015 01:22:59] 2921/3000 | D  9.084024e-004 [- ]
[12/11/2015 01:22:59] 2931/3000 | D  9.084024e-004 [- ]
[12/11/2015 01:22:59] 2941/3000 | D  9.084024e-004 [- ]
[12/11/2015 01:22:59] 2951/3000 | D  9.084024e-004 [- ]
[12/11/2015 01:22:59] 2961/3000 | D  9.084024e-004 [- ]
[12/11/2015 01:22:59] 2971/3000 | D  9.084024e-004 [- ]
[12/11/2015 01:22:59] 2981/3000 | D  9.084024e-004 [- ]
[12/11/2015 01:22:59] 2991/3000 | D  9.084024e-004 [- ]
[12/11/2015 01:22:59] Duration       : 00:00:00.3142646
[12/11/2015 01:22:59] Value initial  : D  4.125000e+001
[12/11/2015 01:22:59] Value final    : D  8.948371e-004 (Best)
[12/11/2015 01:22:59] Value change   : D -4.124910e+001 (-100.00 %)
[12/11/2015 01:22:59] Value chg. / s : D -1.312560e+002
[12/11/2015 01:22:59] Iter. / s      : 9546.09587
[12/11/2015 01:22:59] Iter. / min    : 572765.7522
[12/11/2015 01:22:59] --- Minimization finished

val wopt : DV = DV [|2.99909306f; 0.50039643f|]

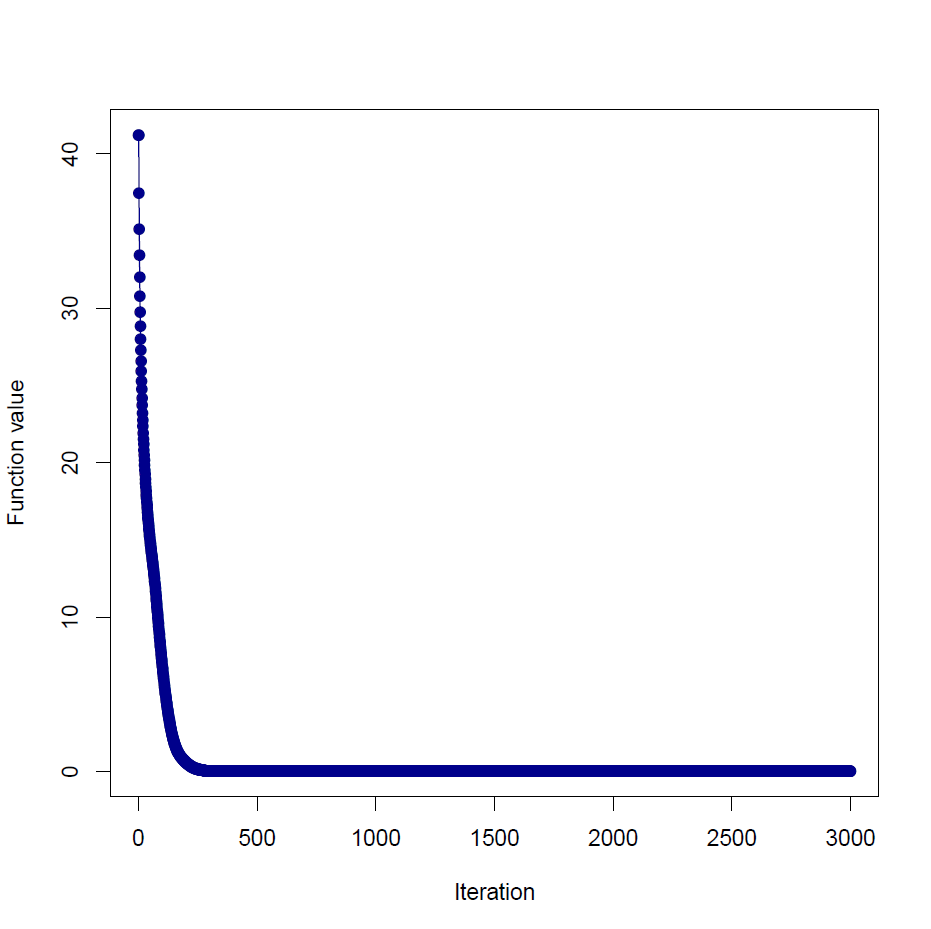
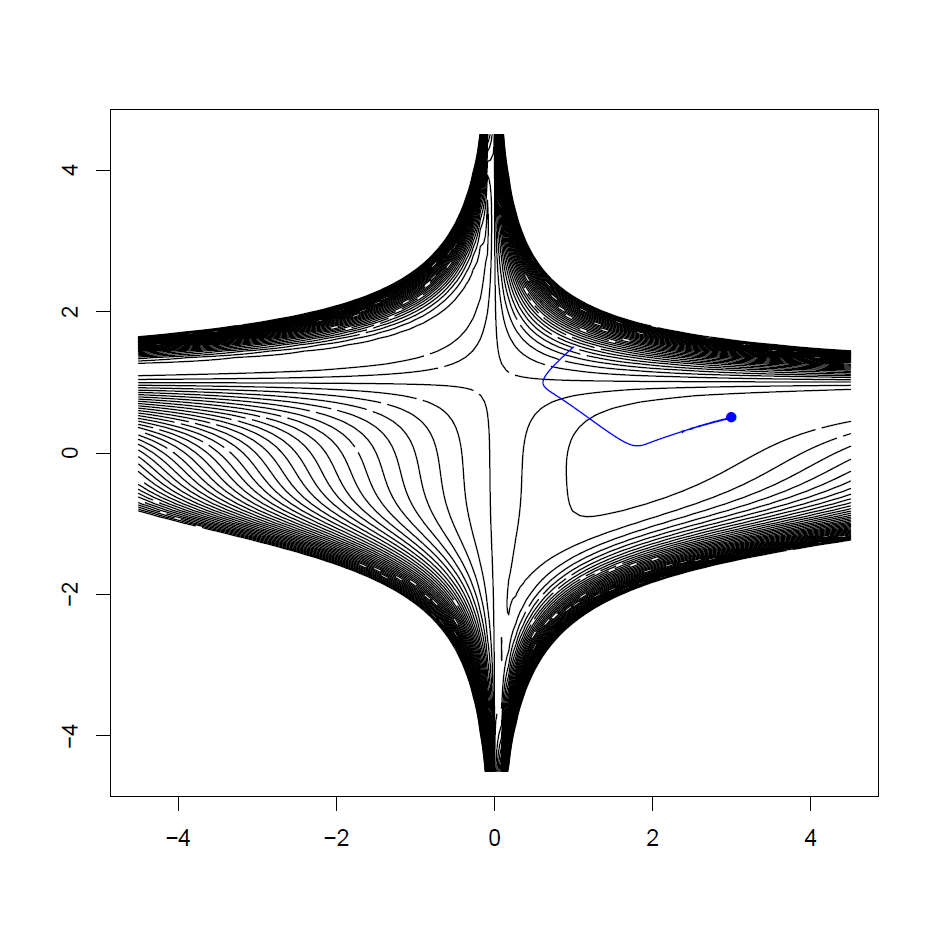
Each instantiation of gradient-based optimization is controlled through a collection of parameters, using the Hype.Params type.

If you do not supply any parameters to optimization, the default parameter set Params.Default is used. The default parameters look like this:

 1: 
 2: 
 3: 
 4: 
 5: 
 6: 
 7: 
 8: 
 9: 
10: 
11: 
12: 
13: 
14: 
15: 

module Params =
     let Default = {Epochs = 100
                    LearningRate = LearningRate.DefaultRMSProp
                    Momentum = NoMomentum
                    Loss = L2Loss
                    Regularization = Regularization.DefaultL2Reg
                    GradientClipping = NoClip
                    Method = GD
                    Batch = Full
                    EarlyStopping = NoEarly
                    ImprovementThreshold = D 0.995f
                    Silent = false
                    ReturnBest = true
                    ValidationInterval = 10
                    LoggingFunction = fun _ _ _ -> ()}

If you want to change only a specific element of the parameter type, you can do so by extending the Params.Default value and overwriting only the parts you need to change, such as this:

1: 
2: 
3: 
4: 

let p = {Params.Default with
            Epochs = 5000
            LearningRate = LearningRate.AdaGrad (D 0.001f)
            Momentum = Nesterov (D 0.9f)}

Optimization method

1: 
2: 
3: 
4: 
5: 
6: 
7: 
8: 

type Method =
    | GD          // Gradient descent
    | CG          // Conjugate gradient
    | CD          // Conjugate descent
    | NonlinearCG // Nonlinear conjugate gradient
    | DaiYuanCG   // Dai & Yuan conjugate gradient
    | NewtonCG    // Newton conjugate gradient
    | Newton      // Exact Newton

Learning rate

 1: 
 2: 
 3: 
 4: 
 5: 
 6: 
 7: 
 8: 
 9: 
10: 
11: 
12: 
13: 
14: 
15: 
16: 

type LearningRate =
    | Constant    of D         // Constant
    | Decay       of D * D     // 1 / t decay, a = a0 / (1 + kt). Initial value, decay rate
    | ExpDecay    of D * D     // Exponential decay, a = a0 * Exp(-kt). Initial value, decay rate
    | Schedule    of DV        // Scheduled learning rate vector, its length overrides Params.Epochs
    | Backtrack   of D * D * D // Backtracking line search. Initial value, c, rho
    | StrongWolfe of D * D * D // Strong Wolfe line search. lmax, c1, c2
    | AdaGrad     of D         // Adagrad. Initial value
    | RMSProp     of D * D     // RMSProp. Initial value, decay rate
    static member DefaultConstant    = Constant (D 0.001f)
    static member DefaultDecay       = Decay (D 1.f, D 0.1f)
    static member DefaultExpDecay    = ExpDecay (D 1.f, D 0.1f)
    static member DefaultBacktrack   = Backtrack (D 1.f, D 0.0001f, D 0.5f)
    static member DefaultStrongWolfe = StrongWolfe (D 1.f, D 0.0001f, D 0.5f)
    static member DefaultAdaGrad     = AdaGrad (D 0.001f)
    static member DefaultRMSProp     = RMSProp (D 0.001f, D 0.9f)

Momentum

1: 
2: 
3: 
4: 
5: 
6: 

type Momentum =
    | Momentum of D // Default momentum
    | Nesterov of D // Nesterov momentum
    | NoMomentum
    static member DefaultMomentum = Momentum (D 0.9f)
    static member DefaultNesterov = Nesterov (D 0.9f)

Gradient clipping

1: 
2: 
3: 
4: 

type GradientClipping =
    | NormClip of D // Norm clipping
    | NoClip
    static member DefaultNormClip = NormClip (D 1.f)

Finally, looking at the API reference and the source code of the optimization module can give you a better idea of the optimization algorithms currently implemented.

• Home

• Optimization
• Training

• Regression
• Neural Networks
• Recurrent Neural Nets
• Hamiltonian MCMC